题目内容
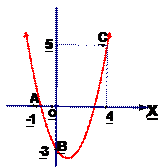
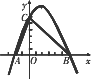
已知如图,二次函数的图象与x轴相交于A、B两点,A、B两点分别在原点两侧,抛物线与y轴正半轴交于点C,若OA∶OB∶OC=1∶3∶3,且△ABC的面积为24,求二次函数的表达式.
答案:
解析:
解析:
|
分析:根据已知条件可以确定A、B、C三点的坐标,由于点A、B在x轴上,所以可利用y=a(x-x1)(x-x2)来求表达式. 解:设OA=x,则OB=OC=3x,根据△ABC的面积为24,可得x=2,所以A、B、C三点的坐标为A(-2,0)、B(6,0)、C(0,6),设所求抛物线的表达式为y=a(x-6)(x+2)(a≠0),将C(0,6)代入,解得a=- 所以二次函数的表达式为 y=- |

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
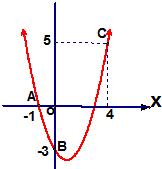 16、已知如图,二次函数y=ax2+bx+c的图象过A、B、C三点
16、已知如图,二次函数y=ax2+bx+c的图象过A、B、C三点

 x+c的图像过A、B、C三点
x+c的图像过A、B、C三点