Question

已知抛物线y＝ax²＋x＋2.

1.当a＝－1时，求此抛物线的顶点坐标和对称轴

2.若代数式－x²＋x＋2的值为正整数，求x的值；

3.若a是负数时，当a＝a₁时，抛物线y＝ax²＋x＋2与x轴的正半轴相交于点M(m，0)；当a＝a₂时，抛物线y＝ax²＋x＋2与x轴的正半轴相交于点N(n，0). 若点M在点N的左边，试比较a₁与a₂的大小.

 

Answer 1

【答案】

 

1.当a=-1时，y=-x²+x+2，∴a=-1,b=1,c=2.

　∴抛物线的顶点坐标为(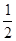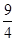，)，对称轴为直线x=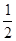.……2分

2.∵代数式-x²+x+2的值为正整数，∴函数y=-x²+x+2的值为正整数.

又因为函数的最大值为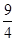，∴y的正整数值只能为1或2.

　　当y=1时，-x²+x+2＝1，解得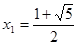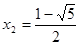，…………3分

　　当y=2时，-x²+x+2＝2，解得x₃=0,x₄=1.……………4分

　　∴x的值为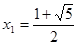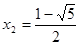，，0或1.

3.当a＜0时，即a₁＜0，a₂＜0.

　　经过点M的抛物线y=a₁x²+x+2的对称轴为,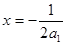

经过点N的抛物线y=a₂x²+x+2的对称轴为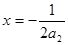.…………5分

∵点M在点N的左边，且抛物线经过点(0,2)

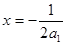∴直线在直线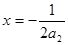的左侧……………6分

∴＜.

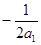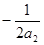∴a₁＜a₂.…………………………………………………………7分

【解析】（1）根据二次函数的顶点坐标和对称轴公式求解。

        （2）根据函数最大值求得x的值。