题目内容
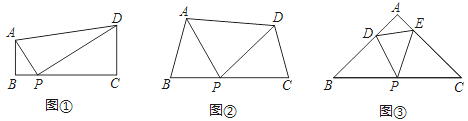
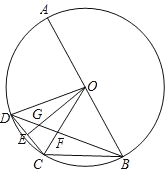
【题目】如图,AB是⊙O的直径,弦BC=OB,点D是![]() 上一动点,点E是CD中点,连接BD分别交OC,OE于点F,G.
上一动点,点E是CD中点,连接BD分别交OC,OE于点F,G.
(1)求∠DGE的度数;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)记△CFB,△DGO的面积分别为S1,S2,若![]() =k,求
=k,求![]() 的值.(用含k的式子表示)
的值.(用含k的式子表示)
【答案】(1)∠DGE=60°;(2)![]() ;(3)
;(3)![]() =
=![]() .
.
【解析】
(1)根据等边三角形的性质,同弧所对的圆心角和圆周角的关系,可以求得∠DGE的度数;
(2)根据题意,三角形相似、勾股定理可以求得![]() 的值;
的值;
(3)根据题意,作出合适的辅助线,然后根据三角形相似、勾股定理可以用含k的式子表示出![]() 的值.
的值.
解:(1)∵BC=OB=OC,
∴∠COB=60°,
∴∠CDB=![]() ∠COB=30°,
∠COB=30°,
∵OC=OD,点E为CD中点,
∴OE⊥CD,
∴∠GED=90°,
∴∠DGE=60°;
(2)过点F作FH⊥AB于点H
设CF=1,则OF=2,OC=OB=3
∵∠COB=60°
∴OH=![]() OF=1,
OF=1,
∴HF=![]() OH=
OH=![]() ,HB=OB﹣OH=2,
,HB=OB﹣OH=2,
在Rt△BHF中,BF![]() ,
,
由OC=OB,∠COB=60°得:∠OCB=60°,
又∵∠OGB=∠DGE=60°,
∴∠OGB=∠OCB,
∵∠OFG=∠CFB,
∴△FGO∽△FCB,
∴$\frac{O F}{B F}=\frac{G F}{C F}$,
∴GF=$\frac{2}{\sqrt{7}}$,
∴![]() =
=![]() .
.
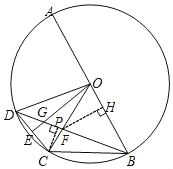
(3)过点F作FH⊥AB于点H,
设OF=1,则CF=k,OB=OC=k+1,
∵∠COB=60°,
∴OH=![]() OF=
OF=![]() ,
,
∴HF=![]() ,HB=OB﹣OH=k+
,HB=OB﹣OH=k+![]() ,
,
在Rt△BHF中,
BF=![]() ,
,
由(2)得:△FGO∽△FCB,
∴![]() ,即
,即![]() ,
,
∴GO![]() ,
,
过点C作CP⊥BD于点P
∵∠CDB=30°
∴PC=![]() CD,
CD,
∵点E是CD中点,
∴DE=![]() CD,
CD,
∴PC=DE,
∵DE⊥OE,
∴![]() =
=![]() =
=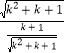 =
=![]()

 名校课堂系列答案
名校课堂系列答案