题目内容
15.四边形ABCD是正方形,以点A为圆心,AB为半径作⊙A,点E是DC边上一点,EF与⊙A相切于点P交BC于点F.(1)如图①,连续AE,AF,求∠EAF的度数.
(2)如图②,若∠CEF=45°,求证:点P是EF的中点.

分析 (1)连结AP,如图①,根据正方形的性质得AB=AD,∠ABC=∠ADC=90°,则可判断BC和CD为⊙A的切线,于是根据切线长定理得ED=EP,FP=FB,则根据角平分线的性质定理的逆定理可判断AE平分∠DAP,即∠1=∠2,同理可得∠3=∠4,所以∠2+∠3=$\frac{1}{2}$∠BAD=45°,即∠EAF=45°;
(2)如图②,由(1)得ED=EP,FP=FB,由∠CEF=45°得CE=CF,由于CD=CB,则DE=BF,则PE=PF,于是可判断点P是EF的中点.
解答 (1)解:连结AP,如图①,
∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠ADC=90°,
∴BC和CD为⊙A的切线,
而EF与⊙A相切于点P,
∴ED=EP,FP=FB,
∴AE平分∠DAP,
∴∠1=∠2,
同理可得∠3=∠4,
∴∠2+∠3=$\frac{1}{2}$∠BAD=$\frac{1}{2}$×90°=45°,
即∠EAF=45°;
(2)证明:如图②,
由(1)得ED=EP,FP=FB,
∵∠CEF=45°,
∴△CEF为等腰直角三角形,
∴CE=CF,
∵四边形ABCD是正方形,
∴CD=CB,
∴CD-CE=CB-CF,即DE=BF,
∴PE=PF,
即点P是EF的中点.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了正方形的性质和切线长定理.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
10.有20筐苹果,以每筐30千克为标准,超过或不足的分别用正、负来表示,记录如下:
(1)20筐苹果中,最重的一筐比最轻的一筐要重多少千克?
(2)与标准质量比较,20筐白菜总计超过或不足多少千克?
(3)若苹果每千克售价5元,则出售这20筐白菜可卖多少元?
| 与标准质量的差(单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| 筐 数 | 1 | 4 | 4 | 4 | 3 | 4 |
(2)与标准质量比较,20筐白菜总计超过或不足多少千克?
(3)若苹果每千克售价5元,则出售这20筐白菜可卖多少元?
7.下列从左边到右边的变形,属于因式分解的是( )
| A. | (x+1)(x-1)=x2-1 | B. | x2-2x+1=x(x•2)+a | C. | (a-b)(b-a)=(b-a)(a-b) | D. | (x-1)(x-3)+1=(x-2)2 |
 (1)请在坐标系中画出二次函数y=x2-2x-1的大致图象.
(1)请在坐标系中画出二次函数y=x2-2x-1的大致图象.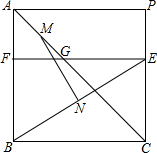 如图,四边形ABCD是边长为8的正方形,点E是CD上的一个动点,EF∥BC分别交AC,AB于点G,F,M,N分别是AG,BE的中点.
如图,四边形ABCD是边长为8的正方形,点E是CD上的一个动点,EF∥BC分别交AC,AB于点G,F,M,N分别是AG,BE的中点.