题目内容
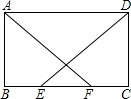已知：如图，在矩形ABCD中，E、F是BC边上的两点，且BE=CF．求证：AF=DE．
证明：∵四边形ABCD是矩形，
∴AB=CD，∠B=∠C=90°；
又∵BE=CF，即BF=CE，
在△ABF和△DCE中：
，
∴△ABF≌△DCE（SAS），
∴AF=DE．
分析：求简单的线段相等，可证线段所在的三角形全等，结合本题，证△ABF≌△DCE即可．
点评：此题考查矩形的性质，全等三角形的判定与性质，简单的线段相等，可以通过全等三角形来证明，要判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．
∴AB=CD，∠B=∠C=90°；
又∵BE=CF，即BF=CE，
在△ABF和△DCE中：
，∴△ABF≌△DCE（SAS），
∴AF=DE．
分析：求简单的线段相等，可证线段所在的三角形全等，结合本题，证△ABF≌△DCE即可．
点评：此题考查矩形的性质，全等三角形的判定与性质，简单的线段相等，可以通过全等三角形来证明，要判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知，如图，在矩形ABCD中，P是边AD上的动点，PE垂直AC于E，PF垂直BD于F，如果AB=3，AD=4，那么（ ）A、PE+PF=
| ||||
B、
| ||||
| C、PE+PF=5 | ||||
| D、3＜PE+PF＜4 |
已知，如图，在矩形ABCD中，M是边BC的中点，AB=3，BC=4，⊙D与直线AM相切于点E，
已知：如图，在矩形ABCD中，AC是对角线．点P为矩形外一点且满足AP=PC，AP⊥PC．PC交AD于点N，连接DP，过点P作PM⊥PD交AD于M．
已知：如图，在矩形ABCD中，AB=4，AD=10，F是AD上一点，CF⊥EF于点F交AB于点E，
已知：如图，在矩形ABCD中，对角线AC与BD相交于点O，BE⊥AC于E，CF⊥BD于F，请你判断BE与CF的大小关系，并说明你的理由．