题目内容
 如图,已知⊙O的弦AB、CD互相垂直,OE垂直于AD于E,证明:BC=2OE.
如图,已知⊙O的弦AB、CD互相垂直,OE垂直于AD于E,证明:BC=2OE.考点:圆周角定理,三角形中位线定理
专题:证明题
分析:连结OA、OB、OC、BD,作OH⊥BC,如图,根据等腰三角形的性质,由OA=OD,OE⊥AD得∠1=
∠AOD,再根据圆周角定理得∠AOD=2∠ABD,则∠1=∠ABD,同理可得∠2=∠BDC,
由CD⊥AB得∠BDF+∠FBD=90°,则∠1+∠2=90°,利用等角的余角相等得∠OAE=∠2,然后证明△OAE≌△BOH,得到OE=BH,于是有BC=2OE.
| 1 |
| 2 |
由CD⊥AB得∠BDF+∠FBD=90°,则∠1+∠2=90°,利用等角的余角相等得∠OAE=∠2,然后证明△OAE≌△BOH,得到OE=BH,于是有BC=2OE.
解答:证明: 连结OA、OB、OC、BD,作OH⊥BC,如图,
连结OA、OB、OC、BD,作OH⊥BC,如图,
∵OA=OD,OE⊥AD,
∴∠1=
∠AOD,
而∠AOD=2∠ABD,
∴∠1=∠ABD,
∵OH⊥BC,
∴BH=CH,∠2=
∠BOC,
而∠BOC=2∠BCD,
∴∠2=∠BDC,
∵CD⊥AB,
∴∠BDF+∠FBD=90°,
∴∠1+∠2=90°,
∵∠1+∠OAE=90°,
∴∠OAE=∠2,
在△OAE和△BOH中
,
∴△OAE≌△BOH,
∴OE=BH,
∴BC=2OE.
 连结OA、OB、OC、BD,作OH⊥BC,如图,
连结OA、OB、OC、BD,作OH⊥BC,如图,∵OA=OD,OE⊥AD,
∴∠1=
| 1 |
| 2 |
而∠AOD=2∠ABD,
∴∠1=∠ABD,
∵OH⊥BC,
∴BH=CH,∠2=
| 1 |
| 2 |
而∠BOC=2∠BCD,
∴∠2=∠BDC,
∵CD⊥AB,
∴∠BDF+∠FBD=90°,
∴∠1+∠2=90°,
∵∠1+∠OAE=90°,
∴∠OAE=∠2,
在△OAE和△BOH中
|
∴△OAE≌△BOH,
∴OE=BH,
∴BC=2OE.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理和三角形全等的判定与性质.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
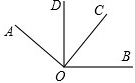 如图,已知∠AOC=∠BOD=90°.
如图,已知∠AOC=∠BOD=90°.