题目内容
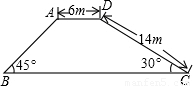
如图，一座堤坝的横截面是梯形，根据图中给出的数据，则坝底宽BC为（精确到0.1m，参加数据：
）
- A.20m
- B.22.9m
- C.24m
- D.25.1m
D
分析：过点A、D分别作BC的垂线AE、DF分别交BC于点E、F，利用三角函数求得DF，FC的长．已知BE=AE，则BC=DF+AD+FC，从而求得坝底宽．
解答：
解：如图所示，过点A、D分别作BC的垂线AE、DF分别交BC于点E、F．
∴△ABE、△CDF均为Rt△．
又∵CD=14，∠DCF=30°．
∴DF=7=AE，
∴cos30°=
=
，
∴FC=7
=12.1．
∴BC=7+6+12.1=25.1m．
故选D．
点评：此题考查了坡角坡角的掌握及综合解直角三角形的运用．
分析：过点A、D分别作BC的垂线AE、DF分别交BC于点E、F，利用三角函数求得DF，FC的长．已知BE=AE，则BC=DF+AD+FC，从而求得坝底宽．
解答：
解：如图所示，过点A、D分别作BC的垂线AE、DF分别交BC于点E、F．∴△ABE、△CDF均为Rt△．
又∵CD=14，∠DCF=30°．
∴DF=7=AE，
∴cos30°=
=，∴FC=7
=12.1．∴BC=7+6+12.1=25.1m．
故选D．
点评：此题考查了坡角坡角的掌握及综合解直角三角形的运用．
练习册系列答案
阅读快车系列答案
相关题目
如图，一座堤坝的横截面是梯形，根据图中给出的数据，求坝高和坝底宽（精确到0.1m）．（参考数据：
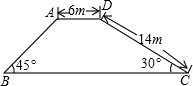如图，一座堤坝的横截面是梯形，根据图中给出的数据，则坝底宽BC为（ ）（精确到0.1m，参加数据：| 2 |
| 3 |
| A、20m | B、22.9m |
| C、24m | D、25.1m |
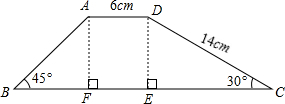如图，一座堤坝的横截面是梯形，根据图中给出的数据，求坝高和坝底宽（精确到0.1m）．（参考数据：
）
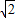=1.414，
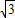=1.732．