题目内容
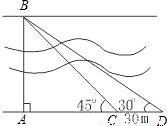
要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使CD=BC，再定出BF的垂线DE，使A、C、E在一条直线上，可以证明△EDC≌△ABC，得到ED=AB，因此测得ED的长就是AB的长（如图）.判定△EDC≌△ABC的理由是
- A.边角边公理
- B.角边角公理
- C.边边边公理
- D.斜边直角边公理
B
试题分析：由已知可以得到∠ABC=∠BDE，又CD=BC，∠ACB=∠DCE，由此根据角边角即可判定△EDC≌△ABC．
∵BF⊥AB，DE⊥BD
∴∠ABC=∠BDE
又∵CD=BC，∠ACB=∠DCE
∴△EDC≌△ABC（ASA）
故选B．
考点：本题考查了全等三角形的判定
点评：解答本题需注意根据垂直定义得到的条件，以及隐含的对顶角相等，观察图形，找着隐含条件是十分重要的．
试题分析：由已知可以得到∠ABC=∠BDE，又CD=BC，∠ACB=∠DCE，由此根据角边角即可判定△EDC≌△ABC．
∵BF⊥AB，DE⊥BD
∴∠ABC=∠BDE
又∵CD=BC，∠ACB=∠DCE
∴△EDC≌△ABC（ASA）
故选B．
考点：本题考查了全等三角形的判定
点评：解答本题需注意根据垂直定义得到的条件，以及隐含的对顶角相等，观察图形，找着隐含条件是十分重要的．
练习册系列答案
导学全程练创优训练系列答案
相关题目
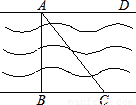
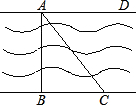如图，河岸护堤AD、BC互相平行，要测量河两岸相对两树A、B的距离，小赵从B点沿垂直AB的BC方向前进，他手中有足够长的米尺和含有30°角的一块三角板．
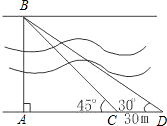要测量河两岸相对两棵树A，B之间的距离，王立同学从A点沿垂直AB的方向前进到C点，测得∠ACB=45°．继续沿AC方向前进30 m到点D，此时沿得∠ADB=30°．依据这些数据能否求出两树之间的距离AB？若能，写出求解过程；不能，说明理由．（
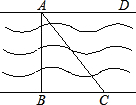如图，河岸护堤AD、BC互相平行，要测量河两岸相对两树A、B的距离，小赵从B点沿垂直AB的BC方向前进，他手中有足够长的米尺和含有30°角的一块三角板．
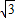取1.73，精确到0.1 m）
