题目内容
某校给参加科普知识竞赛分别获团体一、二、三等奖的3个代表队奖励科普读物若干本,一等奖获得这些奖励读物的一半少一本,二等奖获得剩下的一半多一本,三等奖获得余下的8本书,则这次用来奖励的读物是________本.
32
分析:首先假设参加科普知识竞赛分别获团体一、二、三等奖的3个代表队奖励科普读物的本数依次是x本、y本、z本.
根据题目说明:一等奖获得这些奖励读物的一半少一本,二等奖获得剩下的一半多一本,三等奖获得余下的8本书,可列方程组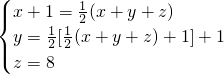
再利用代入法或加减消元法可求出x、y的值,那么x+y+z即为所求值.
解答:设参加科普知识竞赛分别获团体一、二、三等奖的3个代表队奖励科普读物的本数依次是x本、y本、z本.
则由题意得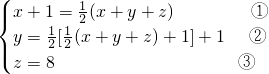
将③代入①②得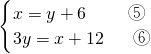
将⑤代入⑥得 3y=y+6+12,即y=9
∴x=15
∴x+y+z=15+9+8=32
故答案为32.
点评:解答此题的关键是列出方程组,用代入消元法或加减消元法求出方程组的解.
分析:首先假设参加科普知识竞赛分别获团体一、二、三等奖的3个代表队奖励科普读物的本数依次是x本、y本、z本.
根据题目说明:一等奖获得这些奖励读物的一半少一本,二等奖获得剩下的一半多一本,三等奖获得余下的8本书,可列方程组
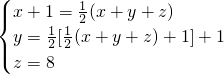
再利用代入法或加减消元法可求出x、y的值,那么x+y+z即为所求值.
解答:设参加科普知识竞赛分别获团体一、二、三等奖的3个代表队奖励科普读物的本数依次是x本、y本、z本.
则由题意得
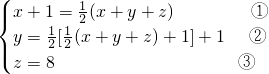
将③代入①②得
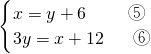
将⑤代入⑥得 3y=y+6+12,即y=9
∴x=15
∴x+y+z=15+9+8=32
故答案为32.
点评:解答此题的关键是列出方程组,用代入消元法或加减消元法求出方程组的解.

练习册系列答案
相关题目

 如图,在Rt△ABC中,∠ACB=90°,斜边AB的中线CD=
如图,在Rt△ABC中,∠ACB=90°,斜边AB的中线CD= ,BC=
,BC= ,则AC的长为________.
,则AC的长为________.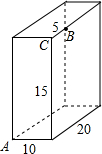 如图,长方体的长为20cm,宽为10cm,高为15cm,点B离点C 5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是多少?
如图,长方体的长为20cm,宽为10cm,高为15cm,点B离点C 5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是多少? 如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中,不正确的是
如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中,不正确的是 =______;(2)
=______;(2)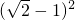 =______.
=______.