题目内容
如图,A(0,1),M(3,2),N(4,4).动点 P 从点 A 出发,沿 y 轴以每秒 1 个单位长的速 度向上移动,且过点 P 的直线 l:y=﹣x+b 也随之移动,设移动时间为 t 秒.若点 M,N 位于直线 l 的异侧,则 t 的取值范围是 .
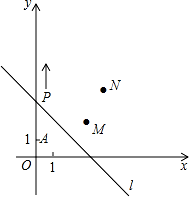
4<t<7
【考点】一次函数图象与几何变换.
【专题】计算题.
【分析】分别求出直线 l 经过点 M、点 N 时的 t 值,即可得到 t 的取值范围.
【解答】解:当直线 y=﹣x+b 过点 M(3,2)时, 2=﹣3+b,
解得:b=5,
5=1+t, 解得 t=4.
当直线 y=﹣x+b 过点 N(4,4)时, 4=﹣4+b,
解得:b=8,
8=1+t, 解得 t=7.
故若点 M,N 位于 l 的异侧,t 的取值范围是:4<t<7. 故答案为:4<t<7.
【点评】本题考查了坐标平面内一次函数的图象与性质,得出直线 l 经过点 M、点 N 时的 t 值是解 题关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目

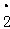 ;④ ;⑤ ;⑥ð.其中无理数的 个数共有( )
;④ ;⑤ ;⑥ð.其中无理数的 个数共有( )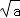 (a﹣
(a﹣ 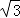 )<0,若 b=2﹣a,则 b 的取值范围是
)<0,若 b=2﹣a,则 b 的取值范围是