题目内容
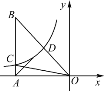
如图,已知反比例函数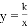 的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于点C,连接AD,OC.若△ABO的周长为
的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于点C,连接AD,OC.若△ABO的周长为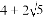 ,AD=2,则△ACO的面积为_________.
,AD=2,则△ACO的面积为_________.
练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
题目内容
如图,已知反比例函数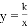 的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于点C,连接AD,OC.若△ABO的周长为
的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于点C,连接AD,OC.若△ABO的周长为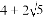 ,AD=2,则△ACO的面积为_________.
,AD=2,则△ACO的面积为_________.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案