题目内容
1.已知关于x的一元二次方程x2-4x+2-k=0有实数根,(1)求k的取值范围;
(2)若k为负整数,且方程两个根均为整数,求出它的根.
分析 (1)由方程的系数结合根的判别式△≥0,可得出8+4k≥0,解之即可得出结论;
(2)由k为负整数可得出k=-2或k=-1,将其代入原方程再解方程即可得出结论.
解答 解:(1)∵关于x的一元二次方程x2-4x+2-k=0有实数根,
∴△=(-4)2-4×1×(2-k)=8+4k≥0,
解得:k≥-2.
(2)∵k≥-2且k为负整数,
∴k=-2或k=-1.
当k=-2时,原方程为x2-4x+4=(x-2)2=0,
解得:x1=x2=2;
当k=-1时,原方程为x2-4x+3=(x-1)(x-3)=0,
解得:x1=1,x2=3.
点评 本题考查了根的判别式以及因式分解法解一元二次方程,解题的关键是:(1)由方程有实数根找出8+4k≥0;(2)由k为负整数得出k值.

练习册系列答案
相关题目
9.若x>y,则下列式子中错误的是( )
| A. | x-2>y-2 | B. | 2-x>2-y | C. | x+2>y+1 | D. | $\frac{x}{3}$>$\frac{y}{3}$ |
16.用配方法解方程x2-2x=3时,原方程应变形为( )
| A. | (x+1)2=2 | B. | (x-1)2=2 | C. | (x+1)2=4 | D. | (x-1)2=4 |
13. 自驾游是当今社会一种重要的旅游方式,五一放假期间小明一家人自驾去灵山游玩,下图描述了小明爸爸驾驶的汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )
自驾游是当今社会一种重要的旅游方式,五一放假期间小明一家人自驾去灵山游玩,下图描述了小明爸爸驾驶的汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )
 自驾游是当今社会一种重要的旅游方式,五一放假期间小明一家人自驾去灵山游玩,下图描述了小明爸爸驾驶的汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )
自驾游是当今社会一种重要的旅游方式,五一放假期间小明一家人自驾去灵山游玩,下图描述了小明爸爸驾驶的汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )| A. | 汽车在0~1小时的速度是60千米/时 | |
| B. | 汽车在2~3小时的速度比0~0.5小时的速度快 | |
| C. | 汽车从0.5小时到1.5小时的速度是80千米/时 | |
| D. | 汽车行驶的平均速度为60千米/时 |
10.下列说法错误的是( )
| A. | 任何数都只有一个立方根 | B. | -0.064的立方根是0.4 | ||
| C. | 16的立方根是$\root{3}{16}$ | D. | -8的立方根是-2 |
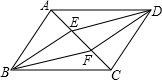 如图,四边形ABCD是平行四边形,且DE∥BF,分别交对角线AC于点E、F,连接EB,FD.
如图,四边形ABCD是平行四边形,且DE∥BF,分别交对角线AC于点E、F,连接EB,FD.