题目内容

探索题：
（x-1）（x+1）=x²-1；
（x-1）（x²+x+1）=x³-1；
（x-1）（x³+x²+x+1）=x⁴-1；
（x-1）（x⁴+x³+x²+x+1）=x⁵-1
…
（1）试求：2⁶+2⁵+2⁴+2³+2²+2+1的值；
（2）判断2²⁰¹⁴+2²⁰¹³+2²⁰¹²+2²⁰¹¹+…+2²+2+1的值的个位上是几？

解：（1）原式=（2-1）（2⁶+2⁵+2⁴+2³+2²+2+1）
=2⁷-1
=127；

（2）原式=（2-1）（2²⁰¹⁴+2²⁰¹³+2²⁰¹²+2²⁰¹¹+…+2²+2+1）
=2²⁰¹⁵-1，
则结果个位上数字为7．
分析：（1）原式变形后，利用得出的规律计算即可得到结果；
（2）原式变形后，利用得出的规律计算得到结果，即可做出判断．
点评：此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．

练习册系列答案

夺冠金卷单元同步测试系列答案

夺冠课时导学案系列答案

发现会考系列答案

发展性评价系列答案

仿真试卷系列答案

非常好冲刺系列答案

非考不可年级衔接总复习系列答案

分层学习检测与评价系列答案

普通高中招生考试命题指导纲要系列答案

高分计划系列答案

相关题目

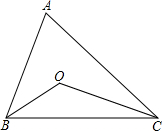（探索题）如图△ABC中，∠ABC，∠ACB的平分线相交于点O．
（1）若∠ABC=40°，∠ACB=80°，求∠BOC；
（2）你能找出∠A与∠BOC之间的数量关系吗？

25、实践探索题：在生产、生活中，我们会经常遇到捆扎圆柱管的问题．下面，我们来探索捆扎时，所需要的绳子的长度（不计接头部分）与圆柱管的半径r之间的关系．
（1）当圆柱管的放置方式是“单层平放”时，截面如图所示：

请你完成下表：

（2）当圆柱管的放置方式是“两层叠放（每一个圆都和至少两个圆外切）”时，截面如图所示：

请你填写下表：

（3）当圆柱管的个数为10时，放置方式有许多种，请你设计一种绳子长度最短的放置方式：画出草图，并计算绳子的长度．

探索题：
观察下列格式

…请你从上述等式中找出规律，并利用这一规律计算（

探索题：
（x-1）（x+1）=x²-1
（x-1）（x²+x+1）=x³-1
（x-1）（x³+x²+x+1）=x⁴-1
（x-1）（x⁴+x³+x²+x+1）=x⁵-1
…
（1）当x=3时，（3-1）（3³+3²+3+1）=3⁴-1=

（2）试求：2⁵+2⁴+2³+2²+2+1的值．
（3）判断2²⁰¹⁰+2²⁰⁰⁹+2²⁰⁰⁸+…+2²+2+1的值的个位数是几？（要有适当的解题过程）

探索题：
观察下列各式
1×3+1=2²；
3×5+1=4²；
2×4+1=3²；
4×6+1=5²；
…
请找出规律，并用含有一个字母的式子表示出来．