题目内容
矩形纸片ABCD的边长AB=8，AD=4，将矩形纸片沿EF折叠，使点A与点C重合，折叠后在某一面着色（如图），则着色部分的面积为
- A.16
- B.
- C.22
- D.8
C
分析：根据折叠的性质可知着色部分的面积等于S矩形ABCD-S△CEF，应先利用勾股定理求得FC的长，进而求得△CEF的面积，代入求值即可．
解答：由折叠的性质可得：CG=AD=4，GF=DF=CD-CF，∠G=90°，
则△CFG为直角三角形，
在Rt△CFG中，FC2-CG2=FG2，
即FC2-42=（8-FC）2，
解得：FC=5，
∴S△CEF=
FC•AD=×5×4=10，
则着色部分的面积为：S矩形ABCD-S△CEF=AB•AD-10=8×4-10=22．
故选C．
点评：本题通过折叠变换考查学生的逻辑思维能力，解决此类问题，应结合题意，由折叠得到相等的边，相等的角，并利用勾股定理求解，要求同学们熟练掌握矩形和三角形的面积公式以及图形面积的转换．
分析：根据折叠的性质可知着色部分的面积等于S矩形ABCD-S△CEF，应先利用勾股定理求得FC的长，进而求得△CEF的面积，代入求值即可．
解答：由折叠的性质可得：CG=AD=4，GF=DF=CD-CF，∠G=90°，
则△CFG为直角三角形，
在Rt△CFG中，FC2-CG2=FG2，
即FC2-42=（8-FC）2，
解得：FC=5，
∴S△CEF=
FC•AD=×5×4=10，则着色部分的面积为：S矩形ABCD-S△CEF=AB•AD-10=8×4-10=22．
故选C．
点评：本题通过折叠变换考查学生的逻辑思维能力，解决此类问题，应结合题意，由折叠得到相等的边，相等的角，并利用勾股定理求解，要求同学们熟练掌握矩形和三角形的面积公式以及图形面积的转换．
练习册系列答案
相关题目
如图，M为矩形纸片ABCD的边AD的中点，将纸片沿BM、CM折叠，使点A落在A1处，点D落在D1处．若∠A1MD1=40°，则∠BMC的度数为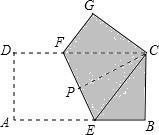
其一面着色．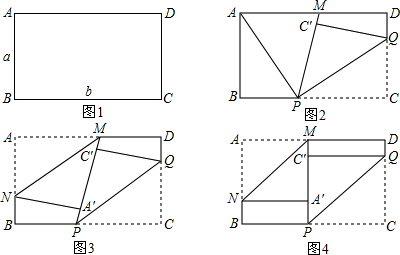
如图，矩形纸片ABCD的边长AB=4，AD=2．将矩形纸片沿EF折叠，使点A与点C重合，折叠后在其一面着色．
已知：如图，矩形纸片ABCD的边AD=3，CD=2，点P是边CD上的一个动点（不与点C重合，把这张矩形纸片折叠，使点B落在点P的位置上，折痕交边AD于点M，折痕交边BC于点N．