题目内容
【题目】我国魏晋时期的数学家刘徽（263年左右）首创“割圆术”，所谓“割圆术”就是利用圆内接正多边形无限逼近圆来确定圆周率，刘徽计算出圆周率
．
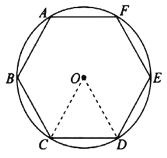
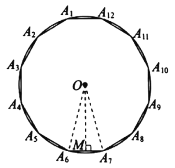
刘徽从正六边形开始分割圆，每次边数成倍增加，依次可得圆内接正十二边形，圆内接正二十四边形，…，割的越细，圆的内接正多边形就越接近圆．设圆的半径为R，圆内接正六边形的周长
，计算
；圆内接正十二边形的周长
，计算
；请写出圆内接正二十四边形的周长
________，计算
________．（参考数据：
，
）
【答案】48Rsin7.5° 3.12
【解析】
根据圆的内接正二十四边形的每条边所对应的圆心角是15°，可知：正二十四边形的周长为：
，进而可求出π的近似值.
∵圆的内接正二十四边形的每条边所对应的圆心角是15°，
∴正二十四边形的周长为：，
∴
，
故答案是：48Rsin7.5°，3.12.
练习册系列答案
相关题目
