题目内容
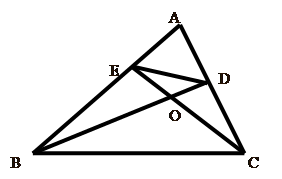
如图中，高BD与CE交于O点，若∠BAC=72°，则∠DOE的度数（ ）分析：由垂直的定义得到∠BDC=∠AEC=90°，再根据三角形内角和定理得∠ACE=180°-∠AEC-∠A=180°-90°-72°=18°，然后根据三角形的外角性质有∠DOE=∠ODC+∠DCO，计算即可得到∠DOE的度数．
解答：解：∵BD、CE分别是边AC，AB上的高，
∴∠BDC=∠AEC=90°，
又∵∠BAC=72°，
∴∠ACE=180°-∠AEC-∠A=180°-90°-72°=18°，
∴∠DOE=∠ODC+∠DCO=90°+18°=108°．
故选C．
∴∠BDC=∠AEC=90°，
又∵∠BAC=72°，
∴∠ACE=180°-∠AEC-∠A=180°-90°-72°=18°，
∴∠DOE=∠ODC+∠DCO=90°+18°=108°．
故选C．
点评：本题考查了三角形的外角性质：三角形的任一外角等于与之不相邻的两内角的和．也考查了垂直的定义以及三角形内角和定理．
练习册系列答案
相关题目
；
