题目内容
韦达定理:若x1,x2为方程ax2+bx+c=0的两根,则x1+x2=-
,x1•x2=
,已知:m和n是方程2x2-5x-3=0的两根,利用以上材料,不解方程,求:
(1)
+
;
(2)m2+n2的值.
| b |
| a |
| c |
| a |
(1)
| 1 |
| m |
| 1 |
| n |
(2)m2+n2的值.
分析:(1)根据m和n是方程2x2-5x-3=0的两根,再根据x1+x2=-
,x1•x2=
,得出m+n和mn的值,再把要求的式子进行变形,再把m+n和mn的值代入即可;
(2)先把m2+n2变形为(m+n)2-2mn,再根据(1)得出的m+n和mn的值,代入进行计算即可.
| b |
| a |
| c |
| a |
(2)先把m2+n2变形为(m+n)2-2mn,再根据(1)得出的m+n和mn的值,代入进行计算即可.
解答:解:(1)∵m和n是方程2x2-5x-3=0的两根,
∴m+n=
,mn=-
,
∴
+
=
=
=-
;
(2)m2+n2
=(m+n)2-2mn
=(
)2-2×(-
)
=
.
∴m+n=
| 5 |
| 2 |
| 3 |
| 2 |
∴
| 1 |
| m |
| 1 |
| n |
| n+m |
| mn |
| ||
-
|
| 5 |
| 3 |
(2)m2+n2
=(m+n)2-2mn
=(
| 5 |
| 2 |
| 3 |
| 2 |
=
| 37 |
| 4 |
点评:此题考查了根与系数的关系,将根与系数的关系与代数式变形相结合是本题的关键,用到的知识点是若方程的两根分别为x1,x2,则x1+x2=-
,x1•x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
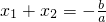 ,
,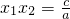 ,已知:m和n是方程2x2-5x-3=0的两根,利用以上材料,不解方程,求:
,已知:m和n是方程2x2-5x-3=0的两根,利用以上材料,不解方程,求: ;
;