Question

16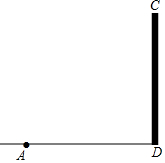．小明同学去大埋旅游时看见一座占塔，他在父母帮助下测得一些数据，首先在地面上的A点测得塔C的仰角为30°，然后沿着向塔的方向前进10m到达B点（点B在线段AD上），则B点测得塔顶C的仰角为45°，请你在图中补画示意图，并求出塔高（精确到0.1m）

Answer 1

分析 设塔高CD为xm，利用正切的定义用x表示出AD、BD，列式计算即可．

解答 解：示意图如图所示：
设塔高CD为xm，
在Rt△CAD中，AD=$\frac{CD}{tan∠CAD}$=$\sqrt{3}$x，
在Rt△CBD中，∠CBD=45°，
∴BD=CD=x，
由题意得，$\sqrt{3}$x-x=10，
解得，x=5$\sqrt{3}$+5≈13.7m，
答：塔高约为13.7m．

点评 本题考查的是解直角三角形的应用-仰角俯角问题，掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键．