题目内容
如图,在▱ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.

证明:(1)∵平行四边形ABCD,
∴AD=CB,∠A=∠C,AD∥CB,
∴∠ADB=∠CBD,
∵ED⊥DB,FB⊥BD,
∴∠EDB=∠FBD=90°,
∴∠ADE=∠CBF,
在△AED和△CFB中,
 ,
,
∴△AED≌△CFB(ASA);
(2)作DH⊥AB,垂足为H,
在Rt△ADH中,∠A=30°,
∴AD=2DH,
在Rt△DEB中,∠DEB=45°,
∴EB=2DH,
∴四边形EBFD为平行四边形,
∴FD=EB,
∴DA=DF.


练习册系列答案
相关题目
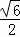


 海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的南偏东60°方向上的B处,求航程AB的值(结果保留根号).
海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的南偏东60°方向上的B处,求航程AB的值(结果保留根号).


 的算术平方根是
的算术平方根是