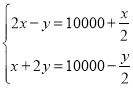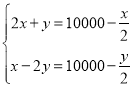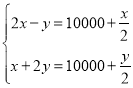题目内容
【题目】如图，抛物线
交
轴正半轴于点
, 顶点
到轴的距离是
，
轴交抛物线于点
,连结
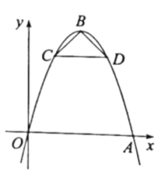
（1）求抛物线的解析式
（2）若
是等腰直角三角形，求
的长．
【答案】（1）
；（2）2
【解析】
（1）根据题意知顶点B（2，4），故设抛物线解析式是：
（a≠0），将点A的坐标代入求得a的值．
（2）如图，作对称轴
交
于点
，设C的横坐标为
，由抛物线的对称性与等腰直角三角形的性质得到的纵坐标，从而表示
的坐标，再代入函数解析式求解的值，从而可得答案．
解：
由题意得，项点坐标为
可设
将A(4．0)代入得4a+4=0，
抛物线的函数表达式为．
如图，作对称轴交于点
抛物线关于直线对称，
是等腰直角三角形，
．
设点的横坐标为，则
的纵坐标是
点的坐标为
将
代入
，
得
(舍去)，
，
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
