题目内容
△ABC∽△A′B′C′且相似比为 ,△A′B′C′∽△A″B″C″且相似比为
,△A′B′C′∽△A″B″C″且相似比为 ,则△ABC与△A″B″C″的相似比为
,则△ABC与△A″B″C″的相似比为
- A.

- B.

- C.

- D.
 或
或
C
分析:设△ABC、△A′B′C′、△A″B″C″的边长分别为x、y、z,根据其相似比等于边长的比即可解答.
解答:设△ABC、△A′B′C′、△A″B″C″的边长分别为x、y、z,
∵△ABC∽△A′B′C′且相似比为 ,△A′B′C′∽△A″B″C″且相似比为
,△A′B′C′∽△A″B″C″且相似比为 ,
,
∴ =
= ,
, =
= ,即x=
,即x=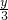 ,z=
,z= ,
,
∴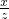 =
= ,即△ABC与△A″B″C″的相似比为
,即△ABC与△A″B″C″的相似比为 ×
× =
= .
.
故选C.
点评:本题考查对相似三角形性质的理解.
分析:设△ABC、△A′B′C′、△A″B″C″的边长分别为x、y、z,根据其相似比等于边长的比即可解答.
解答:设△ABC、△A′B′C′、△A″B″C″的边长分别为x、y、z,
∵△ABC∽△A′B′C′且相似比为
 ,△A′B′C′∽△A″B″C″且相似比为
,△A′B′C′∽△A″B″C″且相似比为 ,
,∴
 =
= ,
, =
= ,即x=
,即x=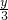 ,z=
,z= ,
,∴
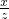 =
= ,即△ABC与△A″B″C″的相似比为
,即△ABC与△A″B″C″的相似比为 ×
× =
= .
.故选C.
点评:本题考查对相似三角形性质的理解.

练习册系列答案
相关题目
 11、如图,△A′BC′是△ABC绕点B顺时针旋转后得到的,则图中AB的对应线段是
11、如图,△A′BC′是△ABC绕点B顺时针旋转后得到的,则图中AB的对应线段是 如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上一个动点,M,N分别是AB,BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )
如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上一个动点,M,N分别是AB,BC的中点,若PM+PN的最小值为2,则△ABC的周长是( ) 20、如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
20、如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F. 9、如图所示,Rt△ABC中,∠C=90°,BE平分∠B交于AC于E,DE垂直平分AB交AB于D,则∠A的度数为( )
9、如图所示,Rt△ABC中,∠C=90°,BE平分∠B交于AC于E,DE垂直平分AB交AB于D,则∠A的度数为( )