题目内容
 9、如图所示,Rt△ABC中,∠C=90°,BE平分∠B交于AC于E,DE垂直平分AB交AB于D,则∠A的度数为( )
9、如图所示,Rt△ABC中,∠C=90°,BE平分∠B交于AC于E,DE垂直平分AB交AB于D,则∠A的度数为( )分析:设∠A=x.根据线段垂直平分线的性质,得AE=BE,根据等边对等角,得∠ABE=∠A=x,根据角平分线定义,得∠ABC=2x,再根据三角形的内角和定理列方程求解.
解答:解:设∠A=x,
∵DE垂直平分AB交AB于D,
∴AE=BE.
∴∠ABE=∠A=x,
∵BE平分∠B交于AC于E,
∴∠ABC=2x,
根据三角形的内角和定理,得
∠A+∠ABC=180°-∠C,
即x+2x=90°,
x=30°.
故选C.
∵DE垂直平分AB交AB于D,
∴AE=BE.
∴∠ABE=∠A=x,
∵BE平分∠B交于AC于E,
∴∠ABC=2x,
根据三角形的内角和定理,得
∠A+∠ABC=180°-∠C,
即x+2x=90°,
x=30°.
故选C.
点评:此题考查了线段垂直平分线的性质、等腰三角形的性质以及三角形的内角和定理;用相等的角进行等量代换,结合三角形的内角和求解,是一种非常重要的方法,注意掌握.

练习册系列答案
相关题目
如图所示,Rt△ABC中,∠C=90°,AB=4,△ABC的面积为
,则tanA+tanB等于( )
| 5 |
| 2 |

A、
| ||
B、
| ||
| C、4 | ||
D、
|
 6、如图所示的Rt△ABC绕直角边AB旋转一周,所得几何体的主视图为( )
6、如图所示的Rt△ABC绕直角边AB旋转一周,所得几何体的主视图为( ) 9、如图所示,Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于D,交AB于点E.当∠B=30°时,图中一定相等的线段错误的有( )
9、如图所示,Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于D,交AB于点E.当∠B=30°时,图中一定相等的线段错误的有( ) 如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.
如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.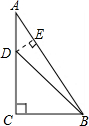 已知:如图所示,Rt△ABC中,∠C=90°,∠ABC=60°,DC=11,D点到AB的距离为2,求BD的长.
已知:如图所示,Rt△ABC中,∠C=90°,∠ABC=60°,DC=11,D点到AB的距离为2,求BD的长.