Question

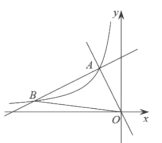
【题目】如图，AB是⊙O的直径，点P是BA延长线上一点，过点P作⊙O的切线PC，切点是C，过点C作弦于E，连接CO，CB．

（1）求证：PD是⊙O的切线；

（2）若，，求PA的长；

（3）试探究线段AB，OE，OP之间的数量关系，并说明理由．

Answer 1

【答案】（1）见解析；（2）；（3）．理由见解析.

【解析】

（1）连接OD，证明∠ODP=90°即可；

（2）由tanB=，可得，可求出AC，BC；再求出CE，OE，由△OCE∽△OPC，可求出OP，PA；

（3）由△OCE∽△OPC得OC2=OEOP，再将代入即可．

（1）证明：连接OD，

∵PC是⊙O的切线，

∴，即，

∵

∴

∴

∴

∵

∴，

∴，

∴PD是⊙O的切线．

（2）如图2，连接AC，

∵AB是⊙O的直径，

∴，

∴

设，，则由勾股定理得：，解得：，

，，

∵，即，

∴，，

在中，，，

∴，

∵

∴，即，

∴，．

（3）

如图2，∵PC切⊙O于C，

∴，

∴

∴，即

∵

∴

即．