题目内容
（1998•广东）以半径为1的圆内接正三角形、正方形、正六边形的边心距为三边作三角形，则（ ）A．不能构成三角形
B．这个三角形是等腰三角形
C．这个三角形是直角三角形
D．这个三角形是钝角三角形
【答案】分析：由于内接正三角形、正方形、正六边形是特殊内角的多边形，可构造直角三角形解答．
解答：解：（1）因为OC=1，所以OD=1×sin30°=
；
（2）因为OB=1，所以OE=1×sin45°=
；
（3）因为OA=1，所以OD=1×cos30°=
．
因为（
）2+（
）2=（
）2，
所以这个三角形是直角三角形．
故选C
点评：解答此题要明确：多边形的半径、边心距、中心角等概念，根据解直角三角形的知识解答．
解答：解：（1）因为OC=1，所以OD=1×sin30°=
；（2）因为OB=1，所以OE=1×sin45°=
；（3）因为OA=1，所以OD=1×cos30°=
．因为（
）2+（）2=（）2，所以这个三角形是直角三角形．
故选C
点评：解答此题要明确：多边形的半径、边心距、中心角等概念，根据解直角三角形的知识解答．
练习册系列答案
相关题目
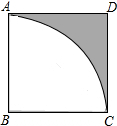（1998•广东）如图，正方形ABCD的边长为1cm，以B为圆心，BA为半径作弧AC，则图中阴影部分面积是
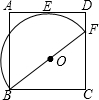（1998•广东）如图，四边形ABCD是正方形，点F在CD上，点O是BF的中点，以BF为直径的半圆与AD相切于点E．