题目内容
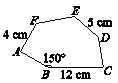
如图,六边形ABCDEF与六边形A′B′C′D′E′F′相似.
求:(1)相似比;
(2)∠A和∠B′的度数;
(3)边CD,EF,A′F′,E′D′的长.
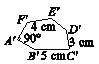
练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
题目内容
如图,六边形ABCDEF与六边形A′B′C′D′E′F′相似.
求:(1)相似比;
(2)∠A和∠B′的度数;
(3)边CD,EF,A′F′,E′D′的长.

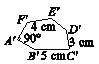
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案