题目内容
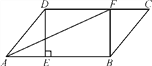
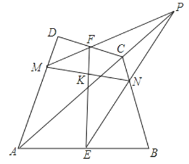
【题目】如图，四边形ABCD中，AB=AD，AD∥BC，∠ABC=60°，∠BCD=30°，BC=6，那么△ACD的面积是（ ）
A.
B.
C.D.
【答案】A
【解析】
如图，过点A作AE⊥BC于E，过点D作DF⊥BC于F．构建矩形AEFD和直角三角形，通过含30度角的直角三角形的性质求得AE的长度，然后由三角形的面积公式进行解答即可．
解：如图，过点A作AE⊥BC于E，过点D作DF⊥BC于F．设AB=AD=x．
又∵AD∥BC，
∴四边形AEFD是矩形，
∴AD=EF=x．
在Rt△ABE中，∠ABC=60°，则∠BAE=30°，
∴BE=
AB=x，
∴DF=AE=
=
x，
在Rt△CDF中，∠FCD=30°，则CF=DFcot30°=
x．
又∵BC=6，
∴BE+EF+CF=6，即x+x+x=6，
解得 x=2
∴△ACD的面积是：ADDF=x×x=
×22=
，
故选：A．
练习册系列答案
53随堂测系列答案
相关题目
