题目内容

若△ABC内切圆的切点将该圆圆周分为7：8：9三条弧，则△ABC的最小内角为（ ）
A．55°
B．50°
C．45°
D．30°
【答案】分析：根据切线的性质定理和四边形的内角和定理，知三个内角分别和三条弧所对的圆心角互补．所以要求最小的内角，只需求得最大的圆心角．
解答：解：∵最大的圆心角是360°×=135°，
∴最小的内角是45°．故选C．
点评：能够发现三个内角和三条弧所对的圆心角的关系是解题的关键．
练习册系列答案
相关题目
精英家教网如图，若等边△ABC的边长为2
3
cm，内切圆O分别切三边于D，E，F，则阴影部分的面积是（　　）
A、2π
B、π
C、
1
2
π
D、
1
3
π
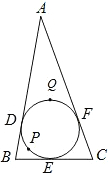精英家教网如图，△ABC的内切圆分别切
.
AB
、
.
BC
、
.
AC
于D、E、F三点，其中P、Q两点分别在
DE
、
DF
上．若∠A=30°，∠B=80°，∠C=70°，则弧长
DPE
与弧长
DQF
的比值为（　　）
A、
2
3
B、
8
7
C、
4
3
D、
8
3
（2007•西城区二模）若等边△ABC的边长为6cm长，内切圆O分别切三边于D、E、F，则阴影部分的面积是（　　）
（2009•自贡）如图，若等边△ABC的边长为6cm，内切圆⊙O分别切三边于点D，E，F，则阴影部分的面积是（　　）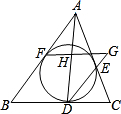
精英家教网如图，△ABC的内切圆分别切BC、CA、AB于点D、E、F，过点F作BC的平行线分别交直线DA、DE于点H、G．问：图中除由切线长定理可知AF=AE，BF=BD，CD=CE外，还有相等的线段吗？若有，请指出来，并加以证明．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网