题目内容
把函数y=-2x+3的图象向下平移4个单位后的函数图象的解析式为
- A.y=-2x+7
- B.y=-6x+3
- C.y=-2x-1
- D.y=-2x-5
C
分析：图象的变换体现在自变量和函数的变化，向下平移4个单位就是将y→y+4，从而得解．
解答：把函数y=-2x+3的图象向下平移4个单位后的函数图象的解析式为y+4=-2x+3，即为y=-2x-1．
故选C．
点评：本题主要考查了求对数函数解析式及图象的变换，属于基础题．
分析：图象的变换体现在自变量和函数的变化，向下平移4个单位就是将y→y+4，从而得解．
解答：把函数y=-2x+3的图象向下平移4个单位后的函数图象的解析式为y+4=-2x+3，即为y=-2x-1．
故选C．
点评：本题主要考查了求对数函数解析式及图象的变换，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（1）在学习《二次函数的图象和性质》时，我们从“数”和“形”两个方面对二次函数y=x2和y=（x+3）2进行了研究，现在让我们重温这一过程．
①填表（表中阴影部分不需填空）：
②从对应点的位置看，函数y=x2的图象与函数y=（x+3）2的图象的位置有什么关系？
（2）借鉴（1）中研究的经验，解决问题：
①把函数y=2x的图象向______（填“左”或“右”）平移______个单位长度可以得到函数y=2x+6的图象．
②直接写出函数y=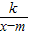
（k、m是常数，k≠0，m＞0）的两条不同类型的性质．
①填表（表中阴影部分不需填空）：
| x | … | -6 | -5 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | … | |
| y=x2 | … | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | … | |||
| y=（x+3）2 | … | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | … |
（2）借鉴（1）中研究的经验，解决问题：
①把函数y=2x的图象向______（填“左”或“右”）平移______个单位长度可以得到函数y=2x+6的图象．
②直接写出函数y=
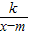（k、m是常数，k≠0，m＞0）的两条不同类型的性质．
（1）在学习《二次函数的图象和性质》时，我们从“数”和“形”两个方面对二次函数y=x2和y=（x+3）2进行了研究，现在让我们重温这一过程．
①填表（表中阴影部分不需填空）：
②从对应点的位置看，函数y=x2的图象与函数y=（x+3）2的图象的位置有什么关系？
（2）借鉴（1）中研究的经验，解决问题：
①把函数y=2x的图象向______（填“左”或“右”）平移______个单位长度可以得到函数y=2x+6的图象．
②直接写出函数y=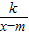
（k、m是常数，k≠0，m＞0）的两条不同类型的性质．
①填表（表中阴影部分不需填空）：
| x | … | -6 | -5 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | … | |
| y=x2 | … | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | … | |||
| y=（x+3）2 | … | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | … |
（2）借鉴（1）中研究的经验，解决问题：
①把函数y=2x的图象向______（填“左”或“右”）平移______个单位长度可以得到函数y=2x+6的图象．
②直接写出函数y=
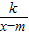（k、m是常数，k≠0，m＞0）的两条不同类型的性质．