Question

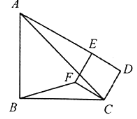
【题目】如图，四边形中，是对角线，以为边向四边形内部作正方形，连接，则的长为________．

Answer 1

【答案】3．

【解析】

连接CE，由等腰直角三角形的性质得出AC＝BC＝3，∠ACB＝45°，由勾股定理得出AD＝，由正方形的性质得出DE＝CD＝3，∠DCF＝90°，∠ECF＝45°，CE＝CF，求出AE＝AD﹣DE＝6，证明△BCF∽△ACE，得出，即可得出结果．

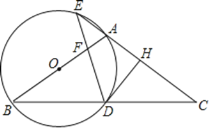
连接CE，如图所示：

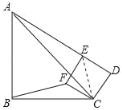
∵∠ABC＝90°，AB＝BC＝3，

∴AC＝BC＝3，∠ACB＝45°，

∵∠D＝90°，CD＝3，

∴AD＝，

∵四边形CDEF是正方形，

∴DE＝CD＝3，∠DCF＝90°，∠ECF＝45°，CE＝CF，

∴AE＝AD﹣DE＝6，

∴∠ACB＝∠ECF，

∴∠BCF＝∠ACE，

∵，

∴△BCF∽△ACE，

∴，

∴；

故答案为3．