题目内容
这是一个著名定理的一种说理过程:将四个如图1所示的直角三角形经过平移、旋转、对称变换运动,拼成如图2所示的中空的四边形ABCD.
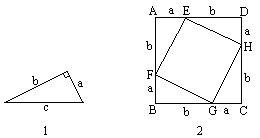
(1)请说明:四边形ABCD和EFGH都是正方形;
(2)结合图形说明等式a2+b2=c2成立,并用适当的文字叙述这个定理的结论.
答案:
解析:
提示:
解析:
|
解:(1)在四边形ABCD中,有∠A=∠B=∠C=∠D= 在四边形EFGH中,有EF=FG=GH=HE=c,∠HEF= (2)在如图中,由于正方形ABCD的面积-4个直角三角形的面积=正方形EFGH的面积因此(a+b)2-4× 即:a2+2ab+b2-2ab=c2 所以:a2+b2=c2 这个定理的结论是:直角三角形中,两条直角边长的平方的和等于斜边长的平方. |
提示:
|
思路与技巧:(1)关键是要说明四边形ABCD和EFGH的四条边相等,四个角都是直角;(2)关键是从面积关系入手,寻找字母a、b、c之间的关系. 评注:著名定理本身的推导方法并不复杂,只要我们认真学好数学基础知识,注意培养自己的创新思维能力,也许会从中受到一些启发,有所发明创造. |

练习册系列答案
相关题目
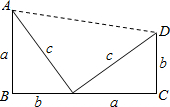 (2010•南浔区模拟)利用图中图形的有关面积的等量关系都能证明数学中一个十分著名的定理,此证明方法就是美国第二十任总统伽菲尔德最先完成的,人们为了纪念他,把这一证法称为“总统”证法.这个定理称为
(2010•南浔区模拟)利用图中图形的有关面积的等量关系都能证明数学中一个十分著名的定理,此证明方法就是美国第二十任总统伽菲尔德最先完成的,人们为了纪念他,把这一证法称为“总统”证法.这个定理称为 在我们的生活中处处有数学的身影,请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理
在我们的生活中处处有数学的身影,请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理