题目内容
在四边形ABCD中，对角线AC、BD相交于点O，且| AD |
| BC |
| AO |
| AC |
分析：由
=
，根据相等向量的大小相等，方向相同，即可证得四边形ABCD是平行四边形；在根据平行四边形的对角线互相平分即可求得k的值．
| AD |
| BC |
解答：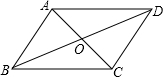
解：∵
=
，
∴AD∥BC，AD=BC，
∴四边形ABCD是平行四边形，
∴OA=OC=
AC，
∴
=
，
∵
=k•
，
∴k=
．
故答案为：
．
解：∵| AD |
| BC |
∴AD∥BC，AD=BC，
∴四边形ABCD是平行四边形，
∴OA=OC=
| 1 |
| 2 |
∴
| AO |
| 1 |
| 2 |
| AC |
∵
| AO |
| AC |
∴k=
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：此题考查了相等向量的意义：大小相等，方向相同．还考查了平行四边形的判定与性质．解此题的关键是正确理解相等向量的意义．
练习册系列答案
相关题目
11、如图所示，在四边形ABCD中，BD是它的一条对角线，若∠1=∠2，∠A=55°16′，则∠ADC=
如图，在四边形ABCD中，AD=BC，P是对角线BD的中点，M是边DC的中点，N是边AB的中点．△MPN是什么三角形？为什么？