题目内容
(2013•响水县一模)如图甲,在平面直角坐标系中,A、B的坐标分别为(4,0)、(0,3),抛物线y=
x2+bx+c经过点B,且对称轴是直线x=-
.
(1)求抛物线对应的函数解析式;
(2)将图甲中的△ABO沿x轴向左平移得到△DCE(如图乙),当四边形ABCD是菱形时,请说明点C和点D都在该抛物线上.
(3)在(2)中,若点M是抛物线上的一个动点(点M不与点C、D重合),通过M作MN∥y轴交直线CD于N,设点M的横坐标为t,MN的长度为l,求l与t之间的函数解析式.并求当为何值时,以M、N、C、E为顶点的四边形是平行四边形.

| 3 |
| 4 |
| 5 |
| 2 |
(1)求抛物线对应的函数解析式;
(2)将图甲中的△ABO沿x轴向左平移得到△DCE(如图乙),当四边形ABCD是菱形时,请说明点C和点D都在该抛物线上.
(3)在(2)中,若点M是抛物线上的一个动点(点M不与点C、D重合),通过M作MN∥y轴交直线CD于N,设点M的横坐标为t,MN的长度为l,求l与t之间的函数解析式.并求当为何值时,以M、N、C、E为顶点的四边形是平行四边形.

分析:(1)把点B的坐标代入抛物线解析式、联合对称轴x=-
列出关于系数b、c的方程组,通过解方程组来求它们的值;
(2)由平移的性质易求点C、D的坐标,将它们的坐标分别代入抛物线解析式进行验证即可;
(3)根据点C、D的坐标易求直线CD的解析式为y=-
x-
.根据已知条件知点M、N的横坐标都是t,则l的值就是点M、N的纵坐标之差.由平行四边形的对边相等的性质推知MN=CE=3,利用所求的l与t间的函数式可以求得相应的t的值.
| b |
| 2a |
(2)由平移的性质易求点C、D的坐标,将它们的坐标分别代入抛物线解析式进行验证即可;
(3)根据点C、D的坐标易求直线CD的解析式为y=-
| 3 |
| 4 |
| 3 |
| 4 |
解答: 解:(1)由已知,得
解:(1)由已知,得
,
解得
.
∴二次函数的解析式为y=
x2+
x+3;
(2)在Rt△ABO中,
∵OA=4,OB=3,
∴AB=5.
又∵四边形ABCD是菱形,
∴BC=AD=AB=5.
∵△ABO沿x轴向左平移得到△DCE,
∴CE=OB=3.
∴C(-5,3)、D(-1,0).
当x=-5时,y=
×(-5)2+
×(-5)+3=3,
当x=-1时,y=
×(-1)3+
×(-1)+3=0,
∴C、D在该抛物线上;
(3)设直线CD的解析式为y=kx+b,则
,
解得
∴y=-
x-
.
∵MN∥y轴,
∴M、N的横坐标均为t.
当M在直线CD的上方时,有l=MN=(
t2+
t+3)-(-
t-
)=
t2+
t+
;
当M在直线CD的下方时,有l=MN=(-
t-
)-(
t2+
t+3)=-
t2-
t-
.
∴l与t之间的函数解析式为l=
t2+
t+
或l=-
t2-
t-
.
由于MN∥CE,要使以点M、N、C、E为顶点的四边形是平行四边形,只需MN=CE=3,
当
t2+
t+
=3时,解得t1=-2
-3,t2=2
-3;
当-
t2-
t-
=3时,解得t3=t4=-3.
即当t=-2
-3或2
-3或-3时,以点M、N、C、E为顶点的四边形是平行四边形.
 解:(1)由已知,得
解:(1)由已知,得
|
解得
|
∴二次函数的解析式为y=
| 3 |
| 4 |
| 15 |
| 4 |
(2)在Rt△ABO中,
∵OA=4,OB=3,
∴AB=5.
又∵四边形ABCD是菱形,
∴BC=AD=AB=5.
∵△ABO沿x轴向左平移得到△DCE,
∴CE=OB=3.
∴C(-5,3)、D(-1,0).
当x=-5时,y=
| 3 |
| 4 |
| 15 |
| 4 |
当x=-1时,y=
| 3 |
| 4 |
| 15 |
| 4 |
∴C、D在该抛物线上;
(3)设直线CD的解析式为y=kx+b,则
|
解得
|
∴y=-
| 3 |
| 4 |
| 3 |
| 4 |
∵MN∥y轴,
∴M、N的横坐标均为t.
当M在直线CD的上方时,有l=MN=(
| 3 |
| 4 |
| 15 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 2 |
| 15 |
| 4 |
当M在直线CD的下方时,有l=MN=(-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 15 |
| 4 |
| 3 |
| 4 |
| 9 |
| 2 |
| 15 |
| 4 |
∴l与t之间的函数解析式为l=
| 3 |
| 4 |
| 9 |
| 2 |
| 15 |
| 4 |
| 3 |
| 4 |
| 9 |
| 2 |
| 15 |
| 4 |
由于MN∥CE,要使以点M、N、C、E为顶点的四边形是平行四边形,只需MN=CE=3,
当
| 3 |
| 4 |
| 9 |
| 2 |
| 15 |
| 4 |
| 2 |
| 2 |
当-
| 3 |
| 4 |
| 9 |
| 2 |
| 15 |
| 4 |
即当t=-2
| 2 |
| 2 |
点评:本题综合考查了待定系数法求一次函数、二次函数解析式,平行四边形的性质.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
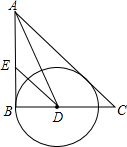 (2013•响水县一模)如图,在△ABC中,∠B=90°,∠A的平分线交BC于D,以D为圆心,DB长为半径作⊙D
(2013•响水县一模)如图,在△ABC中,∠B=90°,∠A的平分线交BC于D,以D为圆心,DB长为半径作⊙D (2013•响水县一模)兴趣小组的同学要测量教学楼前一棵树的高度.在阳光下,一名同学测得一根竖直在地面上的长为1米的竹竿的在地面上的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此台阶上影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则此树高为多少米?
(2013•响水县一模)兴趣小组的同学要测量教学楼前一棵树的高度.在阳光下,一名同学测得一根竖直在地面上的长为1米的竹竿的在地面上的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此台阶上影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则此树高为多少米? (2013•响水县一模)如图,正方形ABCD和EFGC中,正方形EFGC的边长为a,用a的代数式表示阴影部分△AEG的面积为( )
(2013•响水县一模)如图,正方形ABCD和EFGC中,正方形EFGC的边长为a,用a的代数式表示阴影部分△AEG的面积为( )