Question

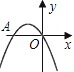
【题目】如图，二次函数y= -x2-2x的图象与x轴交于点A、O，在抛物线上有一点P，满足

S△AOP=3，则点P的坐标是（　　）

A. （-3，-3） B. （1，-3） C. （-3，-3）或（-3，1） D. （-3，-3）或（1，-3）

Answer 1

【答案】D

【解析】分析：根据抛物线的解析式，即可确定点A的坐标，由于OA是定长，根据△AOP的面积即可确定P点纵坐标的绝对值，将其代入抛物线的解析式中，即可求得P点的坐标．

解答：解：抛物线的解析式中，令y=0，得：-x2-2x=0，解得x=0，x=-2；

∴A（-2，0），OA=2；

∵S△AOP=OA?|yP|=3，∴|yP|=3；

当P点纵坐标为3时，-x2-2x=3，x2+2x+3=0，△=4-12＜0，方程无解，此种情况不成立；

当P点纵坐标为-3时，-x2-2x=-3，x2+2x-3=0，

解得x=1，x=-3；

∴P（1，-3）或（-3，-3）；

故选D．