题目内容
 如图,已知:射线PO与⊙O交于A、B两点,PC、PD分别切⊙O于点C、D.
如图,已知:射线PO与⊙O交于A、B两点,PC、PD分别切⊙O于点C、D.(1)请写出两个不同类型的正确结论;
(2)若CD=12,tan∠CPO=
| 1 | 2 |
分析:(1)由切线长定理得①PC=PD,②∠CPO=∠DPA,由垂径定理得③CD⊥BA,④∠CEP=90°,由切割线定理得,⑤PC2=PA•PB;
(2)连接OC,由切线长定理得PC=PD,∠CPO=∠DPA,再由垂径定理得DE,则求得CP,即可得OC,最后根据勾股定理得出OP的长.
(2)连接OC,由切线长定理得PC=PD,∠CPO=∠DPA,再由垂径定理得DE,则求得CP,即可得OC,最后根据勾股定理得出OP的长.
解答: 解:(1)不同类型的正确结论有:
解:(1)不同类型的正确结论有:
①PC=PD,②∠CPO=∠DP,③ACD⊥BA,④∠CEP=90°,⑤PC2=PA•PB;
(2)连接OC
∵PC、PD分别切⊙O于点C、D
∴PC=PD,∠CPO=∠DPA
∴CD⊥AB
∵CD=12
∴DE=CE=
CD=6.
∵tan∠CPO=
,
∴在Rt△EPC中,PE=12
∴由勾股定理得CP=6
∵PC切⊙O于点C
∴∠OCP=90°
在Rt△OPC中,
∵tan∠CPO=
,
∴
=
∴OC=3
,
∴OP=
=15.
 解:(1)不同类型的正确结论有:
解:(1)不同类型的正确结论有:①PC=PD,②∠CPO=∠DP,③ACD⊥BA,④∠CEP=90°,⑤PC2=PA•PB;
(2)连接OC
∵PC、PD分别切⊙O于点C、D
∴PC=PD,∠CPO=∠DPA
∴CD⊥AB
∵CD=12
∴DE=CE=
| 1 |
| 2 |
∵tan∠CPO=
| 1 |
| 2 |
∴在Rt△EPC中,PE=12
∴由勾股定理得CP=6
| 5 |
∵PC切⊙O于点C
∴∠OCP=90°
在Rt△OPC中,
∵tan∠CPO=
| 1 |
| 2 |
∴
| OC |
| PC |
| 1 |
| 2 |
∴OC=3
| 5 |
∴OP=
| OC2+PC2 |
点评:本题考查了切线长定理、勾股定理和垂径定理,是一道综合题,难度较大.

练习册系列答案
相关题目
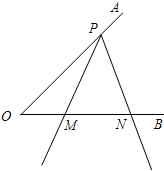 开始,按逆时针方向旋转(∠MPN保持不变)时,M、N两点在射线OB上同时以不同的速度向右平行移动.设OM=x,ON=y(y>x>0),△POM的面积为S.若sinα=
开始,按逆时针方向旋转(∠MPN保持不变)时,M、N两点在射线OB上同时以不同的速度向右平行移动.设OM=x,ON=y(y>x>0),△POM的面积为S.若sinα= 如图,已知:射线PO与⊙O交于A、B两点,PC、PD分别切⊙O于点C、D.
如图,已知:射线PO与⊙O交于A、B两点,PC、PD分别切⊙O于点C、D. ,求PO的长.
,求PO的长. ,求PO的长。
,求PO的长。 
 ,求PO的长.
,求PO的长.