题目内容
5.若直线y=-3x+6与两坐标轴的交点分别是A、B,则△AOB的面积是6.分析 可先求得A、B两点的坐标,则可求得OA和OB,再利用三角形的面积公式计算即可.
解答 解:
在y=-3x+6中,令x=0可得y=6,令y=0可得x=2,
∴A、B两点的坐标为(0,6)和(2,0),
∴OA和OB的长为6和2,
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×6×2=6,
故答案为:6.
点评 本题主要考查一次函数与坐标轴的交点,求得直线与两坐标轴的交点坐标是解题的关键.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
13.正比例函数y=-2x的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
20.下列事件属于必然事件的是( )
| A. | 地面往上抛出的篮球会落下 | B. | 软木塞沉在水底 | ||
| C. | 抛掷一枚硬币,落地后正面朝上 | D. | 买一张彩票中大奖 |
10. 如图,菱形的边长为2,∠ABC=45°,则点A的坐标为( )
如图,菱形的边长为2,∠ABC=45°,则点A的坐标为( )
 如图,菱形的边长为2,∠ABC=45°,则点A的坐标为( )
如图,菱形的边长为2,∠ABC=45°,则点A的坐标为( )| A. | (2,2) | B. | ($\sqrt{2}$,2) | C. | (2,$\sqrt{2}$) | D. | ($\sqrt{2}$,$\sqrt{2}$) |
14. 如图,在?ABCD中,点在AD边上,EF∥CD,交对角线BD于点F,则下列结论中错误的是( )
如图,在?ABCD中,点在AD边上,EF∥CD,交对角线BD于点F,则下列结论中错误的是( )
 如图,在?ABCD中,点在AD边上,EF∥CD,交对角线BD于点F,则下列结论中错误的是( )
如图,在?ABCD中,点在AD边上,EF∥CD,交对角线BD于点F,则下列结论中错误的是( )| A. | $\frac{DE}{AE}$=$\frac{DF}{BF}$ | B. | $\frac{EF}{AB}$=$\frac{DF}{DB}$ | C. | $\frac{EF}{CD}$=$\frac{DF}{BF}$ | D. | $\frac{EF}{CD}$=$\frac{DF}{DB}$ |
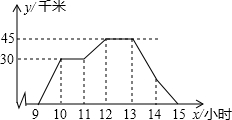 A、B两地路程为45千米,图中折线表示骑车人离A地的路程y与时间x的函数关系,一辆客车10:30从A地出发,沿与骑车人相同的路线以45千米/时的速度往返于A、B两地之间(往返中不停留),以下结论正确的个数有( )
A、B两地路程为45千米,图中折线表示骑车人离A地的路程y与时间x的函数关系,一辆客车10:30从A地出发,沿与骑车人相同的路线以45千米/时的速度往返于A、B两地之间(往返中不停留),以下结论正确的个数有( )


