题目内容
 如图所示,等腰梯形ABCD与等腰梯形A′B′C′D′相似,∠A′=65°,A′B′=6cm,AB=8cm,AD=5cm,试求梯形ABCD的各角的度数与A′D′,B′C′的长.
如图所示,等腰梯形ABCD与等腰梯形A′B′C′D′相似,∠A′=65°,A′B′=6cm,AB=8cm,AD=5cm,试求梯形ABCD的各角的度数与A′D′,B′C′的长.分析:根据相似多边形的对应角相等以及等腰梯形同一底上的两底角相等求出各角的度数;根据相似多边形的对应边成比例列式计算即可求出A′D′,再根据等腰梯形的腰长相等求出B′C′.
解答:解:∵等腰梯形ABCD与等腰梯形A′B′C′D′相似,∠A′=65°,
∴∠A=∠A′=65°,
∠B=∠A=65°,
∠D=∠C=180°-65°=115°;
∵等腰梯形ABCD与等腰梯形A′B′C′D′相似,
∴
=
,
即
=
,
解得A′D′=
cm,
∴B′C′=A′D′=
cm.
∴∠A=∠A′=65°,
∠B=∠A=65°,
∠D=∠C=180°-65°=115°;
∵等腰梯形ABCD与等腰梯形A′B′C′D′相似,
∴
| A′B′ |
| AB |
| A′D′ |
| AD |
即
| 6 |
| 8 |
| A′D′ |
| 5 |
解得A′D′=
| 15 |
| 4 |
∴B′C′=A′D′=
| 15 |
| 4 |
点评:本题考查了相似多边形的性质,主要利用了相似多边形的对应角相等,对应边成比例的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
 如图所示,等腰梯形ABCD中,DC∥AB,对角线AC与BD交于点O,AD=DC,AC=BD=AB.
如图所示,等腰梯形ABCD中,DC∥AB,对角线AC与BD交于点O,AD=DC,AC=BD=AB.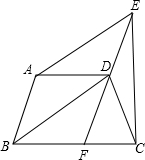 如图所示,等腰梯形ABCD中,AD∥BC,DF∥AB交BC于F点,AE∥BD交FD的延长线于E点.
如图所示,等腰梯形ABCD中,AD∥BC,DF∥AB交BC于F点,AE∥BD交FD的延长线于E点. 20、现有5张如图所示的等腰梯形纸片,打算用其中的若干张来拼成较大的等腰梯形,你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.
20、现有5张如图所示的等腰梯形纸片,打算用其中的若干张来拼成较大的等腰梯形,你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长. 如图所示,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,延长BC至点E,使得CE=AD
如图所示,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,延长BC至点E,使得CE=AD 已知:如图所示,等腰梯形ABCD中,AB∥CD,AD=BC=4,DC=3,△ADE≌△ECB,
已知:如图所示,等腰梯形ABCD中,AB∥CD,AD=BC=4,DC=3,△ADE≌△ECB,