题目内容
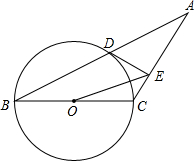 如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.
考点:切线的判定,等腰三角形的性质,三角形中位线定理,圆周角定理
专题:几何综合题
分析:(1)首先连接OD,CD,由以BC为直径的⊙O,可得CD⊥AB,又由等腰三角形ABC的底角为30°,可得AD=BD,即可证得OD∥AC,继而可证得结论;
(2)首先根据三角函数的性质,求得BD,DE,AE的长,然后求得△BOD,△ODE,△ADE以及△ABC的面积,继而求得答案.
(2)首先根据三角函数的性质,求得BD,DE,AE的长,然后求得△BOD,△ODE,△ADE以及△ABC的面积,继而求得答案.
解答: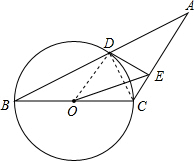 (1)证明:连接OD,CD,
(1)证明:连接OD,CD,
∵BC为⊙O直径,
∴∠BDC=90°,
即CD⊥AB,
∵△ABC是等腰三角形,
∴AD=BD,
∵OB=OC,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∵D点在⊙O上,
∴DE为⊙O的切线;
(2)解:∵∠A=∠B=30°,BC=4,
∴CD=
BC=2,BD=BC•cos30°=2
,
∴AD=BD=2
,AB=2BD=4
,
∴S△ABC=
AB•CD=
×4
×2=4
,
∵DE⊥AC,
∴DE=
AD=
×2
=
,
AE=AD•cos30°=3,
∴S△ODE=
OD•DE=
×2×
=
,
S△ADE=
AE•DE=
×
×3=
,
∵S△BOD=
S△BCD=
×
S△ABC=
×4
=
,
∴S△OEC=S△ABC-S△BOD-S△ODE-S△ADE=4
-
-
-
=
.
 (1)证明:连接OD,CD,
(1)证明:连接OD,CD,∵BC为⊙O直径,
∴∠BDC=90°,
即CD⊥AB,
∵△ABC是等腰三角形,
∴AD=BD,
∵OB=OC,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∵D点在⊙O上,
∴DE为⊙O的切线;
(2)解:∵∠A=∠B=30°,BC=4,
∴CD=
| 1 |
| 2 |
| 3 |
∴AD=BD=2
| 3 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵DE⊥AC,
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
AE=AD•cos30°=3,
∴S△ODE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
∵S△BOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 3 |
∴S△OEC=S△ABC-S△BOD-S△ODE-S△ADE=4
| 3 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
点评:此题考查了切线的判定、三角形中位线的性质、等腰三角形的性质、圆周角定理以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知A样本的数据如下:72,73,76,76,77,78,78,78,B样本的数据恰好是A样本数据每个都加2,则A,B两个样本的下列统计量对应相同的是( )
| A、平均数 | B、标准差 |
| C、中位数 | D、众数 |
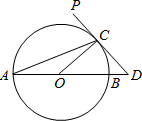 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.