题目内容
1．
如图，AB∥CD，若∠BEC=95°，∠DCE=35°，求∠ABE的度数．
分析 先过点E作EF∥AB，由平行线的传递性可得EF∥CD，再根据平行线的性质即可解答．
解答 解：如图，
过点E作EF∥AB，由平行线的传递性可得EF∥CD，
∵EF∥CD，
∴∠FEC=∠DCE=35°，
∵∠BEC=95°，∠BEF=∠BEC-∠FEC，
∴∠BEF=60°，
∵EF∥AB，
∴∠ABE+∠BEF=180°，
∴∠ABE=180°-∠BEF=180°-60°=120°．
点评 本题考查的是平行线的性质，即两直线平行，同旁内角互补及内错角相等．
练习册系列答案
相关题目
11．下列图形中，既是轴对称又是中心对称的图形是（ ）
| A． | 直角三角形 | B． | 正五边形 | C． | 正六边形 | D． | 等腰梯形 |
12．
如图为某羽毛球场馆的两种计费方案说明．若王老板和朋友们打算在此羽毛球场馆里连续打球6小时，经服务生试算后，告知他们选择包场计费方案会比人数计费方案便宜，则他们至少有多少人参与包场？（ ）
如图为某羽毛球场馆的两种计费方案说明．若王老板和朋友们打算在此羽毛球场馆里连续打球6小时，经服务生试算后，告知他们选择包场计费方案会比人数计费方案便宜，则他们至少有多少人参与包场？（ ）| A． | 6 | B． | 7 | C． | 8 | D． | 9 |
9．下列选项不正确的是（ ）
| A． | 两直线平行，同位角相等 | |
| B． | 对顶角相等 | |
| C． | ∵∠1=∠2，∠2=∠3，∴∠1=∠3 | |
| D． | 两条直线被第三条直线所截，同旁内角互补 |
16．（-x2y3）3•（-x2y2）的结果是（ ）
| A． | -x7y13 | B． | x3y3 | C． | x8y11 | D． | -x7y8 |
6．
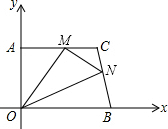在平面直角坐标系中，直角梯形AOBC的位置如图所示，∠OAC=90°，AC∥OB，OA=4，AC=5，OB=6．M、N分别在线段AC、线段BC上运动，当△MON的面积达到最大时，存在一种使得△MON周长最小的情况，则此时点M的坐标为（ ）
在平面直角坐标系中，直角梯形AOBC的位置如图所示，∠OAC=90°，AC∥OB，OA=4，AC=5，OB=6．M、N分别在线段AC、线段BC上运动，当△MON的面积达到最大时，存在一种使得△MON周长最小的情况，则此时点M的坐标为（ ）| A． | （0，4） | B． | （3，4） | C． | （$\frac{5}{2}$，4） | D． | （$\sqrt{3}$，3） |
13．下列各式中正确的是（ ）
| A． | $\sqrt{16}$=±4 | B． | $\root{3}{64}$=4 | C． | $\sqrt{-9}$=3 | D． | $\sqrt{2\frac{1}{4}}$=$\frac{3}{4}$ |
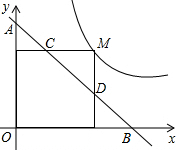如图，M为双曲线y=$\frac{1}{x}$上的一点，过点M作x轴、y轴的垂线，分别交直线y=-x+m于D、C两点，若直线y=-x+m与y轴交于点A，与x轴相交于点B．则AD•BC的值为（ ）