题目内容
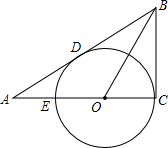 如图,O为Rt△ABC的直角边AC上一点,以O为圆心OC为半径作⊙O切AB于点D,交边AC于点E.
如图,O为Rt△ABC的直角边AC上一点,以O为圆心OC为半径作⊙O切AB于点D,交边AC于点E.(1)若△BDC为等边三角形,试求
| AE |
| AD |
(2)若AC=4,BC=3,求CD的长.
考点:切线的性质
专题:
分析:(1)根据等边三角形的性质得出∠ABC=60°,从而求得∠A=30°,根据30°角所对直角边等于斜边的一半得出BC=
AB,根据切线的性质得出BC=BD,从而求得AD=BC,设BC=x,则AB=2x,AC=
x,根据AD2=AE•AC,即可求得AE═
x,进而即可求得
的值;
(2)连接CD交OB于F,根据勾股定理求得AB=5,根据切线的性质得出BD=BC=3,得出AD=2,根据AD2=AE•AC,求得AE=1,从而求得直径EC,得出半径OC=
再根据勾股定理求得OB,然后根据三角形相似求得CF,即可求得CD的长.
| 1 |
| 2 |
| 3 |
4
| ||
| 3 |
| AE |
| AD |
(2)连接CD交OB于F,根据勾股定理求得AB=5,根据切线的性质得出BD=BC=3,得出AD=2,根据AD2=AE•AC,求得AE=1,从而求得直径EC,得出半径OC=
| 3 |
| 2 |
再根据勾股定理求得OB,然后根据三角形相似求得CF,即可求得CD的长.
解答:解:(1)∵△BDC为等边三角形,
∴∠ABC=60°,
∴∠A=30°,
∴BC=
AB,
∵AC⊥BC,
∴BC是⊙O切线,
∵AB是⊙O切线,
∴BC=BD,
∴AD=BC,
设BC=x,则AB=2x,AC=
x,
∵AD2=AE•AC,
∴(2x)2=AE•
x,
解得AE=
x,
∴
=
=
;
(2)连接CD交OB于F,.
∵在Rt△ABC中,AC=4,BC=3,
∴AB=
=5,
∵BD=BC=3,
∴AD=2,
∵AB是⊙O的切线,
∴AD2=AE•AC,
∴AE=
=1,
∴EC=4-1=3,
∴OC=
,
∵在Rt△OBC中,OC=
,BC=3,
∴OB=
=
,
∵OB垂直平分CD,
∴∠OFC=∠OCB=90°,
∵∠COF=∠BOC,
∴△OCF∽△OBC,
∵
=
∴CF=
∴CD=2CF=
.
∴∠ABC=60°,
∴∠A=30°,
∴BC=
| 1 |
| 2 |
∵AC⊥BC,
∴BC是⊙O切线,
∵AB是⊙O切线,
∴BC=BD,
∴AD=BC,
设BC=x,则AB=2x,AC=
| 3 |
∵AD2=AE•AC,
∴(2x)2=AE•
| 3 |
解得AE=
4
| ||
| 3 |
∴
| AE |
| AD |
| ||||
| x |
4
| ||
| 3 |
(2)连接CD交OB于F,.
∵在Rt△ABC中,AC=4,BC=3,
∴AB=
| AC2+BC2 |
∵BD=BC=3,
∴AD=2,
∵AB是⊙O的切线,
∴AD2=AE•AC,
∴AE=
| 22 |
| 4 |
∴EC=4-1=3,
∴OC=
| 3 |
| 2 |
∵在Rt△OBC中,OC=
| 3 |
| 2 |
∴OB=
| OC2+BC2 |
3
| ||
| 2 |
∵OB垂直平分CD,
∴∠OFC=∠OCB=90°,
∵∠COF=∠BOC,
∴△OCF∽△OBC,
∵
| CF |
| BC |
| OC |
| OB |
∴CF=
3
| ||
| 5 |
∴CD=2CF=
6
| ||
| 5 |
点评:本题考查了切线的性质,等边三角形的性质,勾股定理的应用,直角三角形的性质等,熟练掌握切线的性质是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=
的自变量的取值范围是( )
| 3x-2 |
A、x<
| ||
B、x≤
| ||
C、x>
| ||
D、x≥
|
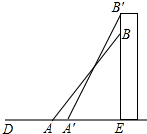 一根竹竿长a米,先像AB靠墙放置,与水平夹角为45°,为了减少占地空间,现将竹竿像A′B′放置,与水平夹角为60°,则竹竿让出多少水平空间( )
一根竹竿长a米,先像AB靠墙放置,与水平夹角为45°,为了减少占地空间,现将竹竿像A′B′放置,与水平夹角为60°,则竹竿让出多少水平空间( )A、(
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、(
|
若a,b互为相反数,c,d互为倒数,|m|=2,则代数式m2-3cd+
的值为( )
| a+b |
| m |
| A、-1 | B、1 | C、-2 | D、1或-7 |
 如图所示,某工厂的大门是抛物线形水泥建筑物,大门的地面宽度为8米,两侧距地面4米高处各有一壁灯,让壁灯间的水平距离为6米,则厂门的高度约为多少?
如图所示,某工厂的大门是抛物线形水泥建筑物,大门的地面宽度为8米,两侧距地面4米高处各有一壁灯,让壁灯间的水平距离为6米,则厂门的高度约为多少?