题目内容
【题目】如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,点D是AC边的中点,E是直线BC上一动点,将线段DE绕点D逆时针旋转90°得到线段DF,连接AF、EF,在点E的运动过程中线段AF的最小值为_____.
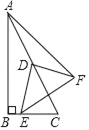
【答案】![]() +1
+1
【解析】
如图,作DM⊥BC于M,FJ⊥DM于J交AB于N.首先说明点F在直线l上运动(直线l与直线AB之间的距离为![]() ),根据垂线段最短可知,当AF⊥直线l时,AF的值最短,最小值为
),根据垂线段最短可知,当AF⊥直线l时,AF的值最短,最小值为![]() .
.
解:如图,作DM⊥BC于M,FJ⊥DM于J交AB于N.
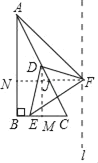
∵Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,
∴AC=2BC=4,AB=![]() BC=2
BC=2![]() ,
,
∵AD=DC.DM∥AB,
∴DM=![]() AB=
AB=![]() ,BM=CM=1,
,BM=CM=1,
易证四边形BMJN是矩形,
∴JN=BM=1,
∵∠FDJ+∠EDM=90°,∠EDM+∠DEM=90°,
∴∠FDJ=∠DEM,∵∠FJD=∠DME=90°,
∴△FJD≌△DME(AAS),
∴FJ=DM=![]() ,
,
∴FN=FJ+JN=1+![]() ,
,
∴点F在直线l上运动(直线l与直线AB之间的距离为![]() +1),
+1),
根据垂线段最短可知,当AF⊥直线l时,AF的值最短,最小值为:![]() +1,
+1,
故答案为:![]() +1.
+1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目