题目内容
已知△ABC:(1)如图1,BO、CO分别为∠ABC,∠ACB的平分线,相交于O.
①如果∠ABC=50°,则∠OBC=______度;
②试说明∠BOC=90°+ ∠A.
∠A.
(2)知识扩展:如图2,若BP、CP分别是∠ABC与∠ACB的外角平分线,相交于点P,设∠A=x°,求∠BPC度数(用含x的代数式表示).

解:(1)①∵BO平分∠ABC,
∴∠OBC= ∠ABC=25°;
∠ABC=25°;
②∵OB、OC分别为∠ABC,∠ACB的平分线,
∴∠ABC=2∠OBC,∠ACB=2∠OCB.
∵∠A=180°-(∠ABC+∠ACB),
∴∠A=180°-2(∠OBC+∠OCB),
∴∠A=180°-2(180°-∠BOC),
∴∠A=-180°+2∠BOC,
∴2∠BOC=180°+∠A,
∴∠BOC=90°+ ∠A.
∠A.
(2)∵BP、CP分别是∠ABC与∠ACB的外角平分线,
∴∠CBP= ∠CBM,∠BCP=
∠CBM,∠BCP= ∠BCN,
∠BCN,
∴∠CBP+∠BCP
= ∠CBM+
∠CBM+ ∠BCN
∠BCN
= (∠CBM+∠BCN)
(∠CBM+∠BCN)
= (∠A+∠ACB+∠A+∠ABC)
(∠A+∠ACB+∠A+∠ABC)
= (180°+∠A),
(180°+∠A),
∴∠BPC=180°-(∠CBP+∠BCP)
=180°- (180°+∠A)
(180°+∠A)
=90°- ∠A
∠A
=90°- x°.
x°.
分析:(1)①根据角平分线的定义进行求解;②根据三角形的内角和定理以及角平分线的定义进行证明.
(2)根据三角形的内角和定理及其推论以及角平分线的定义进行证明.
点评:此题综合运用了三角形的内角和定理及其推论和角平分线的定义.
∴∠OBC=
 ∠ABC=25°;
∠ABC=25°;②∵OB、OC分别为∠ABC,∠ACB的平分线,
∴∠ABC=2∠OBC,∠ACB=2∠OCB.
∵∠A=180°-(∠ABC+∠ACB),
∴∠A=180°-2(∠OBC+∠OCB),
∴∠A=180°-2(180°-∠BOC),
∴∠A=-180°+2∠BOC,
∴2∠BOC=180°+∠A,
∴∠BOC=90°+
 ∠A.
∠A.(2)∵BP、CP分别是∠ABC与∠ACB的外角平分线,
∴∠CBP=
 ∠CBM,∠BCP=
∠CBM,∠BCP= ∠BCN,
∠BCN,∴∠CBP+∠BCP
=
 ∠CBM+
∠CBM+ ∠BCN
∠BCN=
 (∠CBM+∠BCN)
(∠CBM+∠BCN)=
 (∠A+∠ACB+∠A+∠ABC)
(∠A+∠ACB+∠A+∠ABC)=
 (180°+∠A),
(180°+∠A),∴∠BPC=180°-(∠CBP+∠BCP)
=180°-
 (180°+∠A)
(180°+∠A)=90°-
 ∠A
∠A=90°-
 x°.
x°.分析:(1)①根据角平分线的定义进行求解;②根据三角形的内角和定理以及角平分线的定义进行证明.
(2)根据三角形的内角和定理及其推论以及角平分线的定义进行证明.
点评:此题综合运用了三角形的内角和定理及其推论和角平分线的定义.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知ABC的三边满足a2+b2+c2-ab-bc-ac=0,则这个三角形的形状是( )
| A、直角三角形 | B、等腰三角形 | C、等腰直角三角形 | D、等边三角形 |
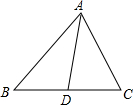 如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )
如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )| A、3<AD<4 | ||||
| B、1<AD<7 | ||||
C、
| ||||
D、
|
已知△ABC中,cosA=
,tgB=1,则△ABC的形状是( )
| 1 |
| 2 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
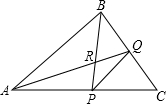 如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于
如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于