题目内容
边长为a的圆内接正三角形的边心距与半径之比是（ ）
分析：过圆心O作圆的内接正n边形的一边AB的垂线OC，垂足是C．连接OA，则在直角△OAC中，∠O=
．OC是边心距，OA即半径．根据三角函数即可求解．
| 180° |
| n |
解答：
解：过圆心O作圆的内接正n边形的一边AB的垂线OC，垂足是C．连接OA，
∵AB=a，
∴AC=
AB=
a，
∵∠AOC=60°，
∴AO=
a，OC=
，
∴边心距与半径的比为1：2．
故选A．
解：过圆心O作圆的内接正n边形的一边AB的垂线OC，垂足是C．连接OA，∵AB=a，
∴AC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOC=60°，
∴AO=
| ||
| 3 |
| ||
| 6 |
∴边心距与半径的比为1：2．
故选A．
点评：本题考查了正多边形和圆的知识，作正多边形和圆的问题时，应连接圆心和正多边形的顶点，作出边心距，得到和中心角一半有关的直角三角形进行求解．
练习册系列答案
相关题目
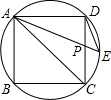如图，在边长为2的圆内接正方形ABCD中，AC是对角线，P为边CD的中点，延长AP交圆于点E．
已知：如图，边长为2的圆内接正方形ABCD中，P为边CD的中点，直线AP交圆于E点．求弦DE的长及△PDE的面积．
∶4