题目内容
【题目】如图,某数学兴趣小组为了测量河对岸l1的两棵古树A、B之间的距离,他们在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则古树A、B之间的距离为m. 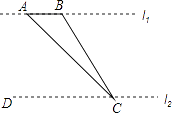
【答案】50﹣ ![]()
【解析】解:如图,过点A作AM⊥DC于点M,过点B作BN⊥DC于点N. 
则AB=MN,AM=BN.
在直角△ACM,∵∠ACM=45°,AM=50m,
∴CM=AM=50m.
∵在直角△BCN中,∠BCN=∠ACB+∠ACD=60°,BN=50m,
∴CN= ![]() =
= ![]() =
= ![]() (m),
(m),
∴MN=CM﹣CN=50﹣ ![]() (m).
(m).
则AB=MN=(50﹣ ![]() )m.
)m.
故答案是:50﹣ ![]() .
.
如图,过点A作AM⊥DC于点M,过点B作BN⊥DC于点N.则AM=BN.通过解直角△ACM和△BCN分别求得CM、CN的长度,则易得MN=AB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
