题目内容
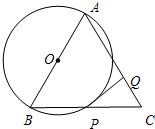6、如图所示，△ABC是等腰三角形，以腰AB为直径作⊙O交底BC于点P，PQ⊥AC于Q，则PQ与⊙O（ ）分析：根据已知条件AB为直径，连接AP和OP，所以AP⊥BC，可知P为BC的中点，O为AB的中点，即OP∥AC；再结合已知条件，可证出OP⊥PQ，则PQ与⊙O相切．
解答：
解：连接AP、OP，
在⊙O中，AB为直径，AP⊥BC，
又∵△ABC是等腰三角形，
∴P点为BC的中点，
又∵O点为AB的中点，
∴OP∥AC，
又PQ⊥AC，
即OP⊥PQ，
∴PQ与⊙O相切．
故选A．
解：连接AP、OP，在⊙O中，AB为直径，AP⊥BC，
又∵△ABC是等腰三角形，
∴P点为BC的中点，
又∵O点为AB的中点，
∴OP∥AC，
又PQ⊥AC，
即OP⊥PQ，
∴PQ与⊙O相切．
故选A．
点评：本题主要考查了等腰三角形的性质及直线和圆的位置关系．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
22、如图所示，△ABC是等边三角形，延长BC至E，延长BA至F，使AF=BE，连接CF、EF，过点F作直线FD⊥CE于D，试发现∠FCE与∠FEC的数量关系，并说明理由．
7、如图所示，△ABC是正三角形，△A1B1 C1的三条边A1B1、BlC1、C1A1交△ABC各边分别于C2、C3，A2、A3，B2、B3．已知A2C3=C2B3=B2A3，且C2C32+B2B32=A2A32．请你证明：AlB1⊥C1A1．
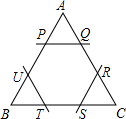如图所示，△ABC是边长为a的正三角形纸张，今在各角剪去一个三角形，使得剩下的六边形PQRSTU为正六边形，则此正六边形的周长为何（ ）| A、2a | ||
| B、3a | ||
C、
| ||
D、
|
12、如图所示，△ABC是等边三角形，AQ=PQ，PR⊥AB于R点，PS⊥AC于S点，PR=PS，则四个结论：①点P在∠A的平分线上；②AS=AR；③QP∥AR；④△BRP≌△QSP，正确的结论是（ ）
（2012•黄陂区模拟）如图所示，△ABC是⊙O的内接正三角形，四边形DEFG是⊙O的内接正方形，EF∥BC，则∠AOF为（ ）