Question

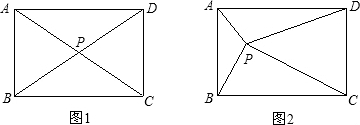
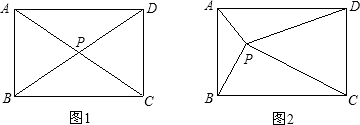
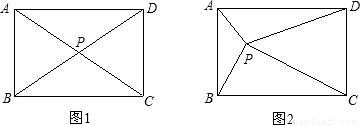
8、点P为矩形ABCD内部或边上的点，若AB＞2BC，那么使△PAD∽△PDC的点P的个数有（　　）

A、1

B、2

C、3

D、4

Answer 1

分析：①注意全等是特殊的相似，所以点P与点B重合符合要求；
②因为AB＞2BC，所以以CD的为直径作圆交AB于点P与P′，根据直径所对的圆周角是直角即可证得；
③在矩形内部也有一点，DP⊥AC即可．

解答：解：①点P与点B重合时，△PAD≌△PDC，可以；
②如图：以CD的为直径作圆交AB于点P与P′，

∴∠DPC=90°，
∵∠A=90°，
∴∠DPC=∠A，
∵AB∥CD，
∴∠1=∠2，
∴△PAD∽△PDC；
同理点P′也是所求点；
③如图：
∵DP⊥AC，
∴∠DPA=CPD=90°，
∴∠CDP+∠DCP=90°，
∵∠CDP+ADP=90°，
∴∠ADP=∠DCP，
∴△PAD∽△PDC．
∴共有4个．
故选D．

点评：此题考查了相似三角形的判定．注意全等是相似的特殊情况．注意直径所对圆周角是直角的定理的应用是关键．解此题还要注意数形结合思想的应用．