题目内容
(1)请在图①的正方形ABCD内,画出一个点P满足∠APB=90°;(2)请在图②的正方形ABCD内(含边),画出使∠APB=60°的所有的点P,并一句话说明理由.(用尺规作图,保留作图痕迹,不写作法)

【答案】分析:(1)正方形对角线的交点符合点P的要求,作对角线即可;
(2)①以AB为边在正方形内作等边△ABP;
②作△ABP的外接圆⊙O,分别与AD、BC交于点E、F,由于在⊙O中,弦AB所对的 上的圆周角均为60°,所以
上的圆周角均为60°,所以 上的所有点均为所求的点P.
上的所有点均为所求的点P.
解答:解:(1)如图①,

连接AC、BD交于点P,则∠APB=90°.
∴点P为所求.(2分)
(2)如图②,画法给分如下:

作△ABP的外接圆⊙O,分别与AD、BC交于点E、F,弧EF上所有的点均可.
理由:同圆中同弧所对的圆周角相等(6分).
点评:此题有点难度,综合利用了正方形的性质和同圆中同弧所对的圆周角相等得知识点.
(2)①以AB为边在正方形内作等边△ABP;
②作△ABP的外接圆⊙O,分别与AD、BC交于点E、F,由于在⊙O中,弦AB所对的
 上的圆周角均为60°,所以
上的圆周角均为60°,所以 上的所有点均为所求的点P.
上的所有点均为所求的点P.解答:解:(1)如图①,

连接AC、BD交于点P,则∠APB=90°.
∴点P为所求.(2分)
(2)如图②,画法给分如下:

作△ABP的外接圆⊙O,分别与AD、BC交于点E、F,弧EF上所有的点均可.
理由:同圆中同弧所对的圆周角相等(6分).
点评:此题有点难度,综合利用了正方形的性质和同圆中同弧所对的圆周角相等得知识点.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
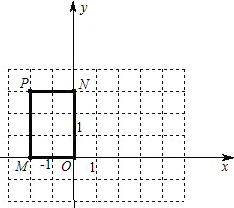 形PMON沿x轴正方向平移4个单位,得到矩形P′M′O′N′(P?P′,M?M′,O?O′,N?N′)
形PMON沿x轴正方向平移4个单位,得到矩形P′M′O′N′(P?P′,M?M′,O?O′,N?N′) 形PMON沿x轴正方向平移4个单位,得到矩形P′M′O′N′(P?P′,M?M′,O?O′,N?N′)
形PMON沿x轴正方向平移4个单位,得到矩形P′M′O′N′(P?P′,M?M′,O?O′,N?N′)

