题目内容
4.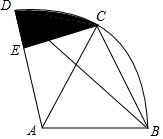 如图所示,在扇形BAD中,点C在$\widehat{BD}$上,且∠BDC=30°,AB=2$\sqrt{2}$,∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )
如图所示,在扇形BAD中,点C在$\widehat{BD}$上,且∠BDC=30°,AB=2$\sqrt{2}$,∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )| A. | π-2 | B. | π-1 | C. | 2π-2 | D. | 2π+1 |
分析 阴影部分的面积=S扇形ACD-S△ACE,根据面积公式计算即可.
解答 解:∵∠BDC=30°,
∴∠BAC=60°,
∵AC=AB,
∴△ABC是等边三角形,
∵∠BAD=105°,
∴∠CAE=105°-60°=45°,
∵CE⊥AD,AC=AB=2$\sqrt{2}$,
∴AE=CE=2,
∴S△ACE=2,
S扇形ACD=$\frac{45•π×(2\sqrt{2})^{2}}{360}$=π,
∴阴影部分的面积为S扇形ACD-S△ACE=π-2,
故选A.
点评 本题考查了三角形和扇形的面积公式及三角函数值,得到阴影部分的面积=S扇形ACD-S△ACE是解题的关键.

练习册系列答案
相关题目
12.一次劳技课上,老师让同学们在一张长为18.宽为16的长方形纸片上,剪下一个腰长为10的等腰三角形,要求等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上,则剪下的等腰三角形的面积可以为( )
| A. | 20 | B. | 40 | C. | 60 | D. | 80 |
9.某小镇在2017年常住人口达到25.8万,用科学记数法表示应为( )
| A. | 25.8×104 | B. | 25.8×105 | C. | 2.58×105 | D. | 2.58×106 |
16.在-3,1,π,0.35 中,无理数是( )
| A. | -3 | B. | $\frac{1}{2}$ | C. | π | D. | 0.35 |
13.-$\frac{1}{2017}$的绝对值是( )
| A. | -2017 | B. | $\frac{1}{2017}$ | C. | 2017 | D. | $-\frac{1}{2017}$ |
14.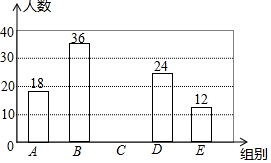 为了关注学生的身心健康发展,减轻学生的学业负担,某校对七年级学生完成家庭作业的时间进行问卷调查,随机抽取了部分学生,记录每个人平均每天完成家庭作业的时间,并将调查数据适当整理,绘制成如下两幅不完整的表和图:
为了关注学生的身心健康发展,减轻学生的学业负担,某校对七年级学生完成家庭作业的时间进行问卷调查,随机抽取了部分学生,记录每个人平均每天完成家庭作业的时间,并将调查数据适当整理,绘制成如下两幅不完整的表和图:
根据以上信息回答下列问题:
(1)a=36,b=0.3,c=120,并将条形统计图补充完整;
(2)这次调查中,学生平均每天完成家庭作业时间的中位数出现在C组;
(3)若该校有在校学生1200人,小明根据上述调查结果,对该校平均每天完成家庭作业的时间在80分钟以上的人数作了如下估计:
∵1200(0.20+0.10)=360,
∴估计该校平均每天完成家庭作业的时间在80分钟以上的人数约为360人.
①上述过程主要体现的数学思想是样本估计总体;
②小明估计的结果是否合理,请说明理由.
 为了关注学生的身心健康发展,减轻学生的学业负担,某校对七年级学生完成家庭作业的时间进行问卷调查,随机抽取了部分学生,记录每个人平均每天完成家庭作业的时间,并将调查数据适当整理,绘制成如下两幅不完整的表和图:
为了关注学生的身心健康发展,减轻学生的学业负担,某校对七年级学生完成家庭作业的时间进行问卷调查,随机抽取了部分学生,记录每个人平均每天完成家庭作业的时间,并将调查数据适当整理,绘制成如下两幅不完整的表和图:| 组别 | 平均每天完成家庭作业的时间(x分钟) | 频数(人数) | 频率 |
| A | x≤40 | 18 | 0.15 |
| B | 40<x≤60 | a | b |
| C | 60<x≤80 | ||
| D | 80<x≤100 | 24 | 0.20 |
| E | x>100 | 12 | 0.10 |
| 合计 | c | 1.00 | |
(1)a=36,b=0.3,c=120,并将条形统计图补充完整;
(2)这次调查中,学生平均每天完成家庭作业时间的中位数出现在C组;
(3)若该校有在校学生1200人,小明根据上述调查结果,对该校平均每天完成家庭作业的时间在80分钟以上的人数作了如下估计:
∵1200(0.20+0.10)=360,
∴估计该校平均每天完成家庭作业的时间在80分钟以上的人数约为360人.
①上述过程主要体现的数学思想是样本估计总体;
②小明估计的结果是否合理,请说明理由.
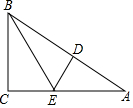 如图,在Rt△ABC中,∠ACB=90°,两条直角边CB、CA的长度分别为6,8,折叠△ABC,使点A、B重合,DE为折痕,连接BE,则cos∠BEC=$\frac{7}{25}$.
如图,在Rt△ABC中,∠ACB=90°,两条直角边CB、CA的长度分别为6,8,折叠△ABC,使点A、B重合,DE为折痕,连接BE,则cos∠BEC=$\frac{7}{25}$.