题目内容
如图,在直角坐标平面内,反比例函数的图象经过点 ,
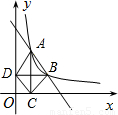
,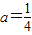 ,其中a>1.过点A作x轴的垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD,DC,CB.
,其中a>1.过点A作x轴的垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD,DC,CB.(Ⅰ)求函数
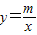 的解析式;
的解析式;(Ⅱ)若△ABD的面积为4,求点B的坐标.
【答案】分析:(1)由已知把点A(1,4)代入y= ,求出m,即得函数y=
,求出m,即得函数y= 的解析式.
的解析式.
(2)连接BD,AC写出点B,D,E的坐标,由此可得DB和AE,再由△ABD的面积为4,可求出a,进而得出点B的坐标.
解答: 解:(Ⅰ)把A(1,4)代入函数解析式,y=
解:(Ⅰ)把A(1,4)代入函数解析式,y= ,得m=4,
,得m=4,
∴所求反比例函数解析式为,y= .
.
(Ⅱ)设BD,AC交于点E,可得B(a, ),D(0,
),D(0, ),E(1,
),E(1, ),
),
∵a>1,
∴DB=a,AE=4- ,由△ABD的面积为4,即
,由△ABD的面积为4,即 a(4-
a(4- ),
),
得a=3,
∴点B的坐标为(3, ).
).
点评:此题考查的知识点是反比例函数综合题,解题的关键是先求出函数解析式,再写出点B,D,E的坐标,由已知面积求出a,从而得出点B的坐标.
 ,求出m,即得函数y=
,求出m,即得函数y= 的解析式.
的解析式.(2)连接BD,AC写出点B,D,E的坐标,由此可得DB和AE,再由△ABD的面积为4,可求出a,进而得出点B的坐标.
解答:
 解:(Ⅰ)把A(1,4)代入函数解析式,y=
解:(Ⅰ)把A(1,4)代入函数解析式,y= ,得m=4,
,得m=4,∴所求反比例函数解析式为,y=
 .
.(Ⅱ)设BD,AC交于点E,可得B(a,
 ),D(0,
),D(0, ),E(1,
),E(1, ),
),∵a>1,
∴DB=a,AE=4-
 ,由△ABD的面积为4,即
,由△ABD的面积为4,即 a(4-
a(4- ),
),得a=3,
∴点B的坐标为(3,
 ).
).点评:此题考查的知识点是反比例函数综合题,解题的关键是先求出函数解析式,再写出点B,D,E的坐标,由已知面积求出a,从而得出点B的坐标.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
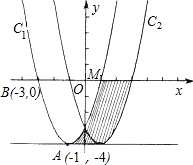 如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)
如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)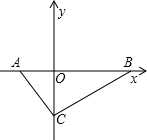 如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=
如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=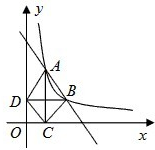 如图,在直角坐标平面内,函数y=
如图,在直角坐标平面内,函数y= 完成下列各题:
完成下列各题: 如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是
如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是