题目内容
如图,四边形OABC是矩形,点B的坐标为(8,6),直线AC和直线OB相交于点M,点P是OA的中点,PD⊥AC,垂足为D.
(1)求直线AC的解析式;
(2)求经过点O、M、A的抛物线的解析式;
 (3)在抛物线上是否存在点Q,使得
(3)在抛物线上是否存在点Q,使得![]() ,若存在,求出点Q的坐标;若不存在,请说明理由.
,若存在,求出点Q的坐标;若不存在,请说明理由.
解:(1)由题意四边形OABC是矩形,点B的坐标为(8,6)可知: A、C两点坐标为A(8,0),C(0,6),设直线AC的解析式y=kx+b,将A(8,0),C(0,6)两点坐标代入y=kx+b,解得 ![]() ,故直线AC的解析式为
,故直线AC的解析式为 ![]() ;
;
(2)由题意可知O(0,0),M(4,3),A(8,0),设经过点O、M、A的抛物线的解析式为y=ax2+bx,将M(4,3),A(8,0),两点坐标代入y=ax2+bx,得 ![]() ,解得
,解得 ![]() ,故经过点O、M、A的抛物线的解析式为
,故经过点O、M、A的抛物线的解析式为 ![]() ;
;
(3)∵△AOC∽△APD,∴ ![]() ,即
,即 ![]() ,解得PD=2.4,AD=3.2,S△PAD:=
,解得PD=2.4,AD=3.2,S△PAD:= ![]() ×PD×AD=
×PD×AD= ![]() ,∵S△PAD:S△QOA=8:
,∵S△PAD:S△QOA=8:
∴S△QOA=12, S△QOA= ![]() ×OA×|yQ|=
×OA×|yQ|= ![]() ×8×|yQ|=12,解得|y|Q=3,又∵点Q在抛物线上,所以
×8×|yQ|=12,解得|y|Q=3,又∵点Q在抛物线上,所以 ![]() =3或
=3或 ![]() =-3,解方程得x1=4,x2=4+4
=-3,解方程得x1=4,x2=4+4 ![]() ,x3=4-4
,x3=4-4 ![]() ,故Q点的坐标为
,故Q点的坐标为![]() 、
、 ![]() 、Q(4,3).
、Q(4,3).
所以![]() 的坐标为:
的坐标为:![]() 、
、![]() 、
、![]()

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.
动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.  在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.
在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.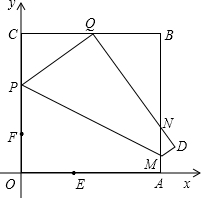
 (2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数
(2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数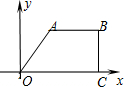 是( )
是( )