Question

【题目】某市在精准扶贫活动中，因地制宜指导农民调整种植结构，增加种植效益．2018年李大伯家在工作队的帮助下，计划种植马铃薯和蔬菜共15亩，预计每亩的投入与产出如下表：（1）如果这15亩地的纯收入要达到54900元，需种植马铃薯和蔬菜各多少亩？（2）如果总投入不超过16000元，则最多种植蔬菜多少亩？该情况下15亩地的纯收入是多少？

	投入（元）	产出（元）
马铃薯	1000	4500
蔬菜	1200	5300

Answer 1

【答案】（1）需种植马铃薯11亩，需种植蔬菜4亩；（2）最多种植蔬菜5亩，该情况下15亩地的纯收入是55500元．

【解析】

（1）设需种植马铃薯x亩，需种植蔬菜y亩，根据等量关系：一共15亩地；这15亩地的纯收入要达到54900元；列出关于x和y的二元一次方程组，解出即可；

（2）设种植马铃薯a亩，则需种植蔬菜（15﹣a）亩，根据“总投入不超过16000元”，列出关于a的一元一次不等式，解出即可．

解：（1）设需种植马铃薯x亩，需种植蔬菜y亩，依题意有

，

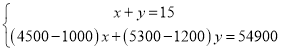解得．

故需种植马铃薯11亩，需种植蔬菜4亩；

（2）设种植马铃薯a亩，则需种植蔬菜（15﹣a）亩，依题意有

1000a+1200（15﹣a）≤16000，

解得a≥10，

15﹣10＝5（亩），

（4500﹣1000）×10+（5300﹣1200）×5

＝35000+20500

＝55500（元）．

答：最多种植蔬菜5亩，该情况下15亩地的纯收入是55500元．